2020年国家提出并部署了“新基建”项目，主要包含“特高压，城际高速铁路和城市轨道交通， 基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩”等．《2020新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域 基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩）总体的人才与就业机会．如图是其中的一个统计图．
请根据图中信息，解答下列问题：
（1）填空：图中2020年“新基建”七大领域预计投资规模的中位数是 300 亿元；
（2）甲，乙两位待业人员，仅根据上面统计图中的数据，从五大细分领域中分别选择了“ 基站建设”和“人工智能”作为自己的就业方向．请简要说明他们选择就业方向的理由各是什么；
（3）小勇对“新基建”很感兴趣，他收集到了五大细分领域的图标，依次制成编号为
，
，
，
，
的五张卡片（除编号和内容外，其余完全相同），将这五张卡片背面朝上，洗匀放好，从中随机抽取一张（不放回），再从中随机抽取一张．请用列表或画状图的方法求抽到的两张卡片恰好是编号为
基站建设）和
（人工智能）的概率．
因式分解：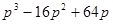
因式分解：
据电力部门统计，每天8︰00至21︰00是用点高峰期，简称“峰时”，21︰00至次日8︰00是用电低谷期，简称“谷时”。为了缓解供电需求紧张的矛盾，我市电力部门拟逐步统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策，具体见下表：
| 时间 |
换表前 |
换表后 |
|
| 峰时（8︰00—21︰00） |
谷时（21︰00—8︰00） |
||
| 电价 |
每度0.52元 |
每度0.55元 |
每度0.30元 |
小明家对换表后最初使用的95度电进行测算，经测算比换表前使用95度电节约了5.9元，问小明家使用“峰时” 电和“谷时” 电分别是多少度?
在如图所示的2005年1月份日历中，
| 星期日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
| 1 |
||||||
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 16 |
17 |
18 |
19 |
20 |
21 |
22 |
| 23 |
24 |
25 |
26 |
27 |
28 |
29 |
| 30 |
31 |
（1）用一个长方形的方框圈出任意3×3个数，如果从左下角到右上角的“对角线”上的3个数字的和为39，那么这9个数的和为；
（2）这个长方形的方框圈出的9个数的和能为216吗？答：（填“能”或“不能”）；
（3）如果任意选择如上的阴影部分，那么其中的四个数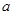
、
、
、
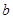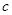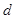又有什么规律呢？请用含的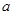、、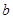、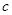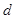等式表示：。
（其中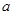、、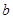、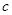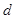四个数之间的大小关系是
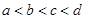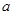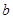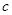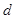，、、、整数）
a※b是新规定的这样一种运算法则：
a※b=a2+2ab，例如3※(-2)=32+2×3×(-2)=－3
(1)试求（-2）※3的值（2）若1※x="3" , 求x的值