某中学举行“中国梦,我的梦”演讲比赛,九年级(1)班的班长和学习委员都想去,于是他们用摸球游戏决定谁去参加,游戏规则是:在一个不透明的袋子里有除数字外完全相同的4个小球,上面分别标有数字1,2,3,4,一人先从袋中随机摸出一个小球,另一个人再从袋中剩下的3个小球中随机摸出一个小球。
(1)请列出所有可能出现的结果;(可考虑用树形图、列表等方法)
(2)若摸出的两个小球上的数字和为偶数,则班长去参赛,请问他能如愿的概率是多少?
(本题8分)已知:如图,点E、F是平行四边行ABCD的对角线AC上的两点,AE=CF。
求证:∠CDF=∠ABE
我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:在四边形ABCD中,取对角线BD的中点O,连接OA、OC.显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.
(1)试说明直线AE是“好线”的理由;
(2)如下图,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,并对画图作适当说明(不需要说明理由).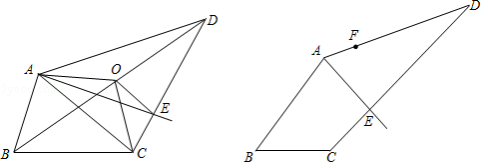
(本题6分)如图,在△ABC中,点E在BC上,CD⊥AB, EF⊥AB,垂足分别为D、F.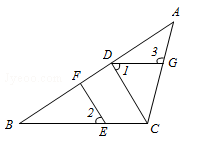
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
一个多边形,它的内角和比外角和的5倍多180°,求这个多边形的边数及内角和度数.
先化简再求值: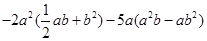 , 其中
, 其中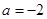 ,
,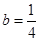 .
.