在平面直角坐标系
中，已知圆心在
轴上，半径为
的圆
位于
轴的右侧，且与轴相切，
（Ⅰ）求圆的方程；
（Ⅱ）若椭圆
的离心率为
，且左右焦点为
，试探究在圆上是否存在点
，使得
为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）
（本题12分）直线l:y=kx＋1与双曲线C: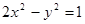
的右支交于不同的两点A,B
（Ⅰ）求实数k的取值范围；
（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若存在，求出k的值；若不存在，说明理由.
（本题12分）已知实数a,b,c,d满足a＋b＋c＋d=3，a2＋2b2＋3c2＋6d2=5，
求证：（Ⅰ）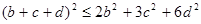
；
（Ⅱ）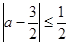
.
（本题12分）如图，设P是圆x2+y2=25上的动点，点D是P在x轴上的投影，M为PD上一点，且|M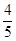D|=
|PD|.
（Ⅰ）当P在圆上运动时，求点M的轨迹C的方程；
（Ⅱ）求过点（3,0）且斜率为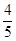的直线被曲线C所截线段的长度.
（本题12分）如图，在长方体ABCD－A1B1C1D1中，E, F分别是棱BC,CC1上的点，CF="AB=2CE," AB:AD:AA1=1:2:4.
（Ⅰ）求异面直线EF与A1D所成角的余弦值；
（Ⅱ）证明AF⊥平面A1ED；
（Ⅲ）求二面角A1－ED－F的正弦值。
（本题12分）已知集合
（Ⅰ）在区间（－4,4）上任取一个实数x，求“x∈A∩B”的概率；
（Ⅱ）设（a,b）为有序实数对，其中a是从集合A中任取的一个整数，b是从集合B中任取的一个整数，求“b－a∈A∪B”的概率.