如图,已知圆 ,点
,点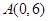 .
.
(1)求圆心在直线 上,经过点
上,经过点 ,且与圆
,且与圆 相外切的圆
相外切的圆 的方程;
的方程;
(2)若过点 的直线
的直线 与圆
与圆 交于
交于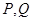 两点,且圆弧
两点,且圆弧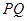 恰为圆
恰为圆 周长的
周长的 ,求直线
,求直线 的方程.
的方程.
已知随机变量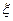 的分布列为
的分布列为
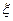 |
-2 |
-1 |
0 |
1 |
2 |
3 |
| P |
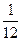 |
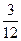 |
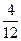 |
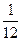 |
 |
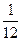 |
分别求出随机变量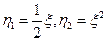 的分布列.
的分布列.
某射手有5发子弹,射击一次命中概率为0.9,如果命中就停止射击,否则一直到子弹用尽,求耗用子弹数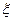 的分布列.
的分布列.
某寻呼台共有客户3000人,若寻呼台准备了100份小礼品,邀请客户在指定时间来领取.假设任一客户去领奖的概率为4%.问:寻呼台能否向每一位顾客都发出奖邀请?若能使每一位领奖人都得到礼品,寻呼台至少应准备多少礼品?
某射手进行射击练习,每射击5发子弹算一组,一旦命中就停止射击,并进入下一组的练习,否则一直打完5发子弹后才能进入下一组练习,若该射手在某组练习中射击命中一次,并且已知他射击一次的命中率为0.8,求在这一组练习中耗用子弹数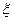 的分布列,并求出
的分布列,并求出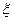 的期望
的期望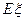 与方差
与方差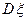 (保留两位小数).
(保留两位小数).
一批产品共100件,其中有10件是次品,为了检验其质量,从中以随机的方式选取5件,求在抽取的这5件产品中次品数分布列与期望值,并说明5件中有3件以上(包括3件)为次品的概率.(精确到0.001)