函数 .
.
(1)若 ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围;
(2)设 ,若对任意
,若对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分14分)如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,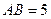 ,AA1=4,点D是AB的中点。
,AA1=4,点D是AB的中点。
(1)求证:AC ⊥ BC1;
(2)求证:AC 1// 平面CDB1;
(3)求多面体 的体积。
的体积。
(本小题满分12分)已知函数
(1)求函数 的最小正周期;
的最小正周期;
(2)当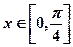 时,求函数f (x) 的最大值与最小值及相应的
时,求函数f (x) 的最大值与最小值及相应的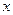 值。
值。
.(本小题满分12分)
(1)设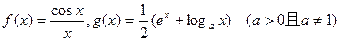 ,求
,求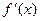 和
和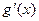 ;
;
(2)设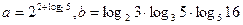 ,求
,求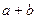 的值。
的值。
已知函数 ,其中
,其中 为大于零的常数.
为大于零的常数.
(Ⅰ)若曲线 在点(1,
在点(1, )处的切线与直线
)处的切线与直线 平行,求
平行,求 的值;
的值;
(Ⅱ)求函数 在区间[1,2]上的最小值.
在区间[1,2]上的最小值.
已知数列 满足
满足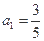 ,
,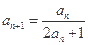 ,
,
(Ⅰ)计算出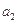 、
、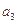 、
、 ;
;
(Ⅱ)猜想数列 通项公式
通项公式
 ,并
,并 用数学归纳法进行证明.
用数学归纳法进行证明.