如图，PA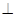
平面ABCD，四边形ABCD为矩形，PA=AB=
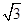，AD=1，点F是PB的中点，点E在边BC上移动．
(I)求三棱锥E—PAD的体积；
(II)试问当点E在BC的何处时，有EF//平面PAC；
(1lI)证明：无论点E在边BC的何处，都有PE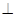AF．
函数
（1）若函数
在
内没有极值点，求
的取值范围；
（2）若对任意的
，不等式
在
上恒成立，求实数
的取值范围．
己知集合
，
，
，若“
”是“
”的充分不必要条件，求
的取值范围．
已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和
个黑球（为正整数）．现从甲、乙两个盒内各任取2个球，若取出的4个球均为黑球的概率为
，求
（1）的值；
（2）取出的4个球中黑球个数大于红球个数的概率．
已知抛物线
的方程为
，点
在抛物线上．
（1）求抛物线的方程；
（2）过点
作直线交抛物线于不同于
的两点
，若直线
分别交直线
于
两点，求
最小时直线
的方程．
如图，在矩形
中，
，点
在边
上，点
在边
上，且
，垂足为
，若将
沿
折起，使点
位于
位置，连接
，得四棱锥
．
(1)求证：平面
平面
；
(2)若
，直线
与平面
所成角的大小为
，求直线
与平面
所成角的正弦值．