设函数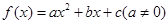
，曲线
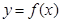通过点(0，2a+3)，且在
处的切线垂直于y轴．
(I)用a分别表示b和c；
(II)当bc取得最大值时，写出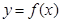的解析式；
(III)在(II)的条件下，若函数
g(x)为偶函数,且当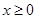
时,
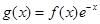，求当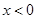
时g(x)的表达式，并求函数g(x)在R上的最小值及相应的x值．
已知函数
（1）若对任意实数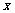
，函数值恒大于零，求实数
的取值范围；
（2）若函数有两个不同的零点，求实数的取值范围．
（本小题满分12分）已知数列
的前n项和为
，点
均在函数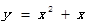
的图像上
（1）求数列的通项公式；
（2）设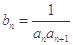
，求数列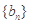
的前n项和
（本小题满分12分）已知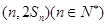
，若
是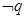
的充分而不必要条件，求实数
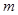的取值范围．
（本小题满分12分）已知等差数列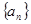
的第二项为8，前10项和为185．
（1）求数列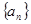的通项公式；
（2）若从数列
通项满足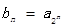
，试求数列的通项公式和前n项的和
．：
（本小题满分12分）设有两个命题，命题P：不等式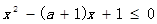
的解集是
；命题：函数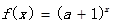
在定义域中是增函数，
（1）若
为真命题时，求a的取值范围；
（2）若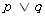
为真命题时，求a的取值范围．