某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为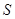 平方米.
平方米.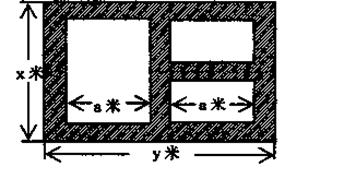
(1)分别写出用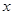 表示
表示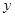 和用
和用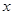 表示
表示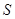 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
设函数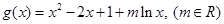 .
.
(1)当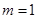 时,求过点
时,求过点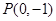 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)若函数 有两个极值点
有两个极值点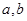 ,且
,且 ,记
,记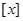 表示不大于
表示不大于 的最大整数,试比较
的最大整数,试比较 与
与 的大小.
的大小.
已知椭圆 的左右焦点分别为
的左右焦点分别为 ,点
,点 为短轴的一个端点,
为短轴的一个端点, .
.
(1)求椭圆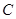 的方程;
的方程;
(2)如图,过右焦点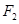 ,且斜率为
,且斜率为 的直线
的直线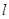 与椭圆
与椭圆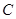 相交于
相交于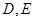 两点,
两点,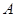 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线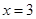 于点
于点 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为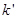 .求证:
.求证: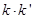 为定值.
为定值.
如图,在三棱锥 中,
中, 面
面 ,
,  ,且
,且 ,
, 为
为 的中点,
的中点, 在
在 上,且
上,且 .
.
(1)求证: ;
;
(2)求平面 与平面
与平面 的夹角的余弦值.
的夹角的余弦值.
甲、乙、丙三位同学彼此独立地从A、B、C、D、E五所高校中,任选2所高校参加自主招生考试(并且只能选2所高校),但同学甲特别喜欢A高校,他除选A校外,在B、C、D、E中再随机选1所;同学乙和丙对5所高校没有偏爱,都在5所高校中随机选2所即可.
(1)求甲同学未选中E高校且乙、丙都选中E高校的概率;
(2)记X为甲、乙、丙三名同学中未参加E校自主招生考试的人数,求X的分布列及数学期望.
已知数列 的前
的前 项和为
项和为 ,首项
,首项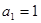 ,且对于任意
,且对于任意 都有
都有 .
.
(1)求 的通项公式;
的通项公式;
(2)设 ,且数列
,且数列 的前
的前 项之和为
项之和为 ,求证:
,求证: .
.