如图,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.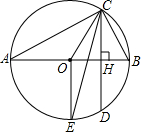
(1)若∠BAC=30°,求证:CD平分OB.
(2)若点E为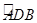 的中点,连接0E,CE.求证:CE平分∠OCD.
的中点,连接0E,CE.求证:CE平分∠OCD.
(3)若⊙O的半径为4,∠BAC=30°,则圆周上到直线AC距离为3的点有多少个?请说明理由.
解方程: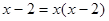 .
.
如图甲,小刚准备在C处牵牛到河边AB处饮水.
(1)请用三角板作出小刚的最短路线(不考虑其它因素),并说明理由;
(2)如图乙,若小刚在C处牵牛到河边AB处饮水,并且必须到河边D处观察河的水质情况,请作出小刚行走的最短路线,并说明理由.
“五一”长假里,弟弟和妈妈从家里出发一同去外婆家,他们走了 小时后,哥哥发现带给外婆的礼品忘在家里了,便立刻带上礼品以每小时
小时后,哥哥发现带给外婆的礼品忘在家里了,便立刻带上礼品以每小时 千米的速度去追,如果弟弟和妈妈每小时行
千米的速度去追,如果弟弟和妈妈每小时行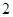 千米.他们从家里到外婆家需要
千米.他们从家里到外婆家需要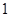 小时
小时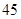 分钟,问哥哥能在弟弟和妈妈到外婆家之前追上他们吗?
分钟,问哥哥能在弟弟和妈妈到外婆家之前追上他们吗?
马和骡子并排走着,背上都驮着包袱,马抱怨说它驮得太多,骡子回答说:“你抱怨什么呢?如果我从你背上拿过一包来,我的负担就是你的两倍,如果你从我背上拿过一包去,你驮的不过和我一样多.”请问马和骡子各驮几个包裹?(假定各包裹的重量相等)
(1)已知关于X的方程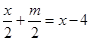 与方程
与方程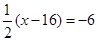 的解相同,求
的解相同,求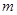 的值.
的值.
(2)若关于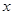 的方程
的方程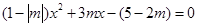 是一元一次方程.求此方程的解.
是一元一次方程.求此方程的解.