如图,在平面直角坐标系中,抛物线经过点A的坐标为(m,m),点B的坐标为(n,-n),且经过原点O,连接OA、OB、AB,线段AB交y轴于点C.已知实数m,n(m<n)分别是方程x2-2x-3=0的两根.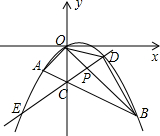
(1)求m,n的值.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD,BD.当△OPC为等腰三角形时,求点P的坐标.
解方程
(1)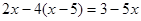
(2)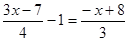
化简
(1)
(2)2(a2b+ab2)-2(a2b-1)+2ab2-2
如图,已知在直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.点P是x轴上的一个动点,设P(x,0)。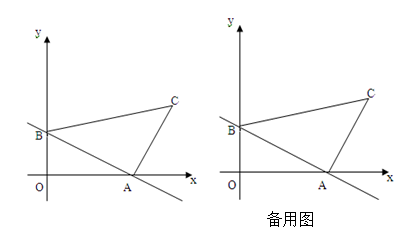
(1)求△ABC的面积;
(2)若△ABP是等腰三角形,求点P的坐标;
(3)是否存在这样的点P,使得|PC-PB|的值最大?如果不存在,请说明理由;如果存在,请在备用图中标出点P的位置。
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E。
证明:DE=BD+CE。
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由。
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并给出证明。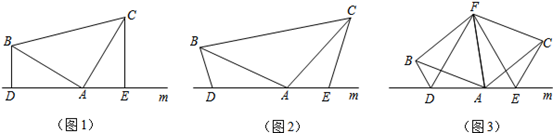
实验中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)购买一个足球、一个篮球各需多少元?
(2)根据实验中学的实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不低于5600但不超过5720元,可以有哪几种购买方案?