老师要求同学们在图①中
内找一点P，使点P到OM、ON的距离相等．
小明是这样做的：在OM、ON上分别截取OA=OB，连结AB，取AB中点P，点P即为所求．
请你在图②中的内找一点P，使点P到OM的距离是到ON距离的2倍．要求：简单叙述做法，并对你的做法给予证明．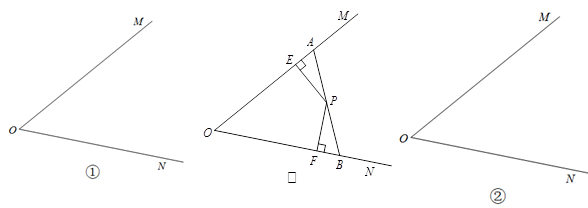
（本题12分）某公司生产的一种健身产品在市场上受到普遍欢迎，每年可在国内、国外市场上全部售完．该公司的年产量为6千件，若在国内市场销售，平均每件产品的利润y1（元）与国内销售量x（千件）的关系为：
y1=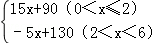
若在国外销售，平均每件产品的利润y2（元）与国外的销售数量t（千件）的关系为
（1）用x的代数式表示t为：t=；当0＜x≤4时，y2与x的函数关系为：y2=；当＜x＜时，y2=100；
（2）当该公司在国内销售量是国外销量的两倍时，问总利润是多少？
（3）该公司每年国内、国外的销售量各为多少时，可使公司每年的总利润最大？最大值为多少？
（本题10分）小颖有20张大小相同的卡片，上面写有20个数字，她把卡片放在一个盒子中搅匀，每次从盒中抽出一张卡片并放回，记录结果如下：
| 实验次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
| 3的倍数的频数 |
5 |
13 |
17 |
26 |
32 |
36 |
39 |
49 |
55 |
61 |
| 3的倍数的频率 |
0.25 |
,0.33 |
0.28 |
0.33 |
0.32 |
0.30 |
,0.31 |
,0.31 |
（1）完成上表；（精确到0.01）
（2）频率随着实验次数的增加，稳定于什么值左右？
（3）从试验数据看，从盒中摸出一张卡片是3的倍数的概率估计是多少？
（4）结合实际问题，根据计算推理可知，从盒中摸出一张卡片是3的倍数的概率应该是多少？
（本题10分）已知二次函数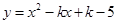
．（1）若此二次函数最小值为-4，求此二次函数解析式；（2）求证：无论
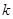取何实数，此二次函数的图像与
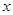轴都有两个交点；（3）有学生研究此二次函数图象性质时发现，无论K取何值此二次函数图一定经过一个定点；你认为正确吗？若认为正确，直接写出此定点坐标，若不正确，说明理由。
（本题10分）
跨江大桥采用了国际上新颖的U型钢构组合拱桥结构，主桥的钢拱在空中划出一道优美的弧线，远远望去像是一弯彩虹横卧于清波之上，大桥的桥拱是抛物线的一部分，位于桥面上方部分的拱高约20米，跨度约120米。如图，
（1）请你建立适当的直角坐标系，求出描述主桥上的钢拱形状的抛物线解析式；
（2）问距离桥拱与桥面交点20米处的支架长为多少米？
（本题8分）有形状、大小和质地都相同的四张卡片，正面分别写有 和一个等式，将这四张卡片背面向上洗匀，从中随机抽取一张（不放回），接着再随机抽取一张.
（1）用画树状图或列表的方法表示抽取两张卡片可能出现的所情况（结果用A，B，C，D表示）.
（2）小明和小强按下面规则做游戏：两人各抽一张卡片,两张卡片上若等式都不成立，则小明胜；若至少有一个等式成立，则小强胜你认为这个游戏公平吗？若公平，请说明理由；若不公平，则这个规则对谁有利？为什么？