在平面直角坐标系xOy中,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,4),D为OC的中点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,4),D为OC的中点.
(1)求m的值;
(2)抛物线的对称轴与 x轴交于点E,在直线AD上是否存在点F,使得以点A、B、F为顶点的三角形与△ADE 相似?若存在,请求出点F的坐标,若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点G,使△GBC中BC边上的高为 ?若存在,求出点G的坐标;若不存在请说明理由.
?若存在,求出点G的坐标;若不存在请说明理由.
化简:(x+1)2﹣x(x+1).
在平面直角坐标系中,抛物线 与
与 轴交于点
轴交于点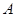 ,
, ,与
,与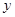 轴交于点
轴交于点 ,直线
,直线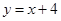 经过
经过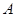 ,
, 两点.
两点.
(1)求抛物线的解析式;
(2)在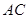 上方的抛物线上有一动点
上方的抛物线上有一动点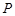 .
.
①如图1,当点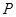 运动到某位置时,以
运动到某位置时,以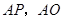 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点
为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点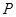 的坐标;21·cn·jy·com
的坐标;21·cn·jy·com
②如图2,过点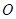 ,
,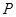 的直线
的直线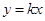 交
交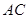 于点
于点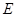 ,若
,若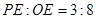 ,求
,求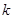 的值.
的值.
如图,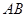 为⊙O的直径,
为⊙O的直径,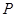 是
是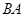 延长线上一点,
延长线上一点,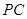 切⊙O于点
切⊙O于点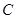 ,
,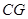 是⊙O的弦,
是⊙O的弦,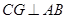 ,垂足为
,垂足为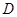 .
.
(1)求证: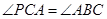 ;
;
(2)过点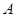 作
作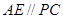 交⊙O于点
交⊙O于点 ,交
,交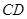 于点
于点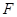 ,连接
,连接 .若
.若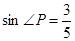 ,
,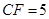 ,求
,求 的长.
的长.
已知关于x的一元二次方程:
(1)试判断原方程根的情况;
(2)若抛物线 与
与 轴交于
轴交于 两点,则
两点,则 ,
, 两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示:
两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示: )
)
某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件 型服装计酬16元,加工1件
型服装计酬16元,加工1件 型服装计酬12元.在工作中发现一名熟练工加工1件
型服装计酬12元.在工作中发现一名熟练工加工1件 型服装和2件
型服装和2件 型服装需4小时,加工3件
型服装需4小时,加工3件 型服装和1件
型服装和1件 型服装需7小时.(工人月工资=底薪+计件工资)
型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件 型服装和1件
型服装和1件 型服装各需要多少小时?
型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工 ,
, 两种型号的服装,且加工
两种型号的服装,且加工 型服装数量不少于
型服装数量不少于 型服装的一半”.设一名熟练工人每月加工
型服装的一半”.设一名熟练工人每月加工 型服装
型服装 件,工资总额为
件,工资总额为 元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?