某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件 型服装计酬16元,加工1件
型服装计酬16元,加工1件 型服装计酬12元.在工作中发现一名熟练工加工1件
型服装计酬12元.在工作中发现一名熟练工加工1件 型服装和2件
型服装和2件 型服装需4小时,加工3件
型服装需4小时,加工3件 型服装和1件
型服装和1件 型服装需7小时.(工人月工资=底薪+计件工资)
型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件 型服装和1件
型服装和1件 型服装各需要多少小时?
型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工 ,
, 两种型号的服装,且加工
两种型号的服装,且加工 型服装数量不少于
型服装数量不少于 型服装的一半”.设一名熟练工人每月加工
型服装的一半”.设一名熟练工人每月加工 型服装
型服装 件,工资总额为
件,工资总额为 元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
如图,在△ACD中,B为AC上一点,且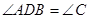 ,
,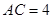 ,
,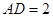 ,
,
求AB的长.
关于x的一元二次方程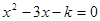 有两个不相等的实数根.
有两个不相等的实数根.
(1)求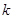 的取值范围;
的取值范围;
(2)若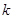 为符合条件的最小整数,求此时方程的根.
为符合条件的最小整数,求此时方程的根.
已知:二次函数的图象经过原点,对称轴是直线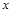 =-2,最高点的纵坐标为4,求:该二次函数解析式。
=-2,最高点的纵坐标为4,求:该二次函数解析式。
如图抛物线过坐标原点O和x轴上另一点E,顶点M为 (2,4);矩形ABCD顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速从图示位置沿x轴正方向匀速平行移动,同时一动点P也以相同速度从点A出发向B匀速移动,设它们运动时间为t秒(0≤t≤3),直线AB与该抛物线交点为N
① 当t= 时,判断点P是否在直线ME上,说明理由;
时,判断点P是否在直线ME上,说明理由;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?说明理由.
如图1,在正方形 中,对角线
中,对角线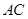 与
与 相交于点
相交于点 ,
, 平分
平分 ,交
,交 于点
于点 .
.
(1)求证: ;
;
(2)点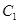 从点
从点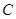 出发,沿着线段
出发,沿着线段 向点
向点 运动(不与点
运动(不与点 重合),同时点
重合),同时点 从点
从点 出发,沿着
出发,沿着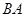 的延长线运动,点
的延长线运动,点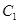 与
与 的运动速度相同,当动点
的运动速度相同,当动点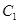 停止运动时,另一动点
停止运动时,另一动点 也随之停止运动.如图2,
也随之停止运动.如图2, 平分
平分 ,交
,交 于点
于点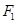 ,过点
,过点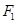 作
作 ,垂足为
,垂足为 ,请猜想
,请猜想 ,
, 与
与 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当 ,
,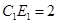 时,求
时,求 的长
的长