已知椭圆的中心在原点,焦点在x轴上,离心率 。它有一个顶点恰好是抛物线
。它有一个顶点恰好是抛物线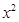 =4y的焦点。过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
=4y的焦点。过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且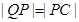 。
。
(Ⅰ)求动点C的轨迹E的方程;
(Ⅱ)设椭圆的左右顶点分别为A,B,直线AC(C点不同于A,B)与直线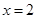 交于点R,D为线段RB的中点。试判断直线CD与曲线E的位置关系,并证明你的结论。
交于点R,D为线段RB的中点。试判断直线CD与曲线E的位置关系,并证明你的结论。
如图,在四棱锥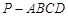 中,
中, 为平行四边形,且
为平行四边形,且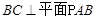 ,
,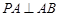 ,
,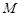 为
为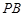 的中点,
的中点,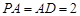 ,
,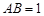 .
.
(Ⅰ)求证: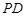 //
//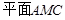 ;
;
(Ⅱ)求三棱锥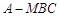 的高.
的高.
气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) |
t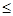 22℃ 22℃ |
22℃< t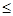 28℃ 28℃ |
28℃< t 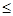 32℃ 32℃ |
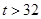 ℃ ℃ |
| 天数 |
6 |
12 |
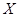 |
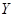 |
由于工作疏忽,统计表被墨水污染,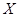 和
和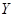 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
(Ⅰ) 若把频率看作概率,求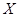 ,
,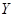 的值;
的值;
(Ⅱ) 把日最高气温高于32℃称为本地区的 “高温天气”,根据已知条件完成下面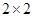 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
| 高温天气 |
非高温天气 |
合计 |
|
| 旺销 |
1 |
||
| 不旺销 |
6 |
||
| 合计 |
附: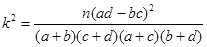
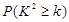 |
0.10 |
0.050 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知各项为正数的等差数列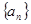 满足
满足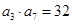 ,
,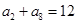 ,且
,且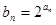 (
(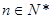 ).
).
(Ⅰ)求数列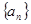 的通项公式;
的通项公式;
(Ⅱ)设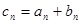 ,求数列
,求数列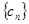 的前n项和
的前n项和 .
.
设函数 .
.
(Ⅰ)当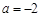 时,解不等式
时,解不等式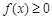 ;
;
(Ⅱ)当 时,不等式
时,不等式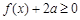 的解集为
的解集为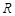 ,求实数
,求实数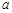 的取值范围.
的取值范围.
直角坐标系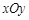 中,曲线
中,曲线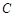 的参数方程为
的参数方程为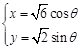 (
(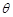 为参数),直线
为参数),直线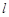 的参数方程为
的参数方程为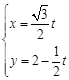 (
(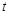 为参数),
为参数),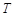 为直线
为直线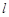 与曲线
与曲线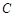 的公共点. 以原点
的公共点. 以原点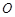 为极点,
为极点,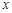 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(Ⅰ)求点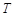 的极坐标;
的极坐标;
(Ⅱ)将曲线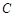 上所有点的纵坐标伸长为原来的
上所有点的纵坐标伸长为原来的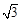 倍(横坐标不变)后得到曲线
倍(横坐标不变)后得到曲线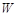 ,过点
,过点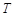 作直线
作直线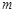 ,若直线
,若直线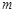 被曲线
被曲线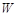 截得的线段长为
截得的线段长为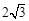 ,求直线
,求直线 的极坐标方程.
的极坐标方程.