在平面直角坐标系中,角α,β的始边为x轴的非负半轴,点 在角α的终边上,点
在角α的终边上,点 在角β的终边上,且
在角β的终边上,且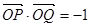
(1)求
(2)求P,Q的坐标并求 的值
的值
在直角坐标系 中,点 到 轴的距离等于点 到点 的距离,记动点 的轨迹为 .
(1)求 的方程;
(2)已知矩形 有三个顶点在 上,证明:矩形 的周长大于 .
甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为 ,乙每次投篮的命中率均为 .由抽签确定第 次投篮的人选,第 次投篮的人是甲、乙的概率各为 .
(1)求第 次投篮的人是乙的概率;
(2)求第 次投篮的人是甲的概率;
(3)已知:若随机变量 服从两点分布,且 , 则 .记前 次(即从第 次到第 次投篮)中甲投篮的次数为 ,求 .
设等差数列 的公差为 ,且 .令 ,记 , 分别为数列 , 的前 项和.
(1)若 , ,求 的通项公式;
(2)若 为等差数列,且 ,求 .
已知函数 .
(1)讨论 的单调性;
(2)证明:当 时, .
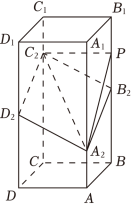
如图,在正四棱柱 中, , .点 , , , 分别在棱 , , , 上, , , .
(1)证明: ;
(2)点 在棱 上,当二面角 为 时,求 .