四棱锥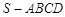 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 .已知
.已知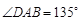 ,
,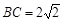 ,
,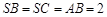 ,
,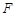 为线段
为线段 的中点.
的中点.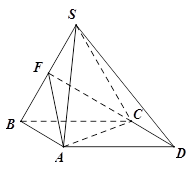
(Ⅰ)求证: 平面
平面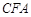 ;
;
(Ⅱ)求面 与面
与面 所成二面角大小.
所成二面角大小.
函数
的部分图象如图所示.
(1)写出
的最小正周期及图中
、
的值;
(2)求
在区间
上的最大值和最小值.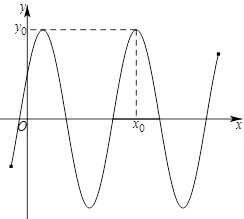
已知
是等差数列,满足
,数列
满足
,且
是等比数列.
(1)求数列
和
的通项公式;
(2)求数列
的前
项和.
设 分别是椭圆 的左、右焦点,过点 的直线交椭圆E于A,B两点,
(1)若
的周长为16,求
;
(2)若
,求椭圆E的离心率.
设函数 ,其中 ;
(1)讨论
在其定义域上的单调性;
(2)当
时,求
取得最大值和最小值时的
的值.
如图,四棱锥
的底面边长为8的正方形,四条侧棱长均为
.点
分别是棱
上共面的四点,平面
平面
,
平面
.
(1)证明:
(2)若
,求四边形
的面积.