如图,在平行四边形ABCD中,点E,F分别是AB,CD的中点.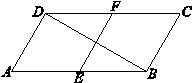
(1)求证：四边形AEFD是平行四边形；(2)若∠A=60°,AB=2AD=4,求BD的长.
如图，在平行四边形
中，
，
，
，垂足为
，
．
（1）求
、
的长；
（2）求
的正切值．
解方程：
．
已知，
，
是
的平分线，点
在上，
．将三角板的直角顶点放置在点处，绕着点旋转，三角板的一条直角边与射线
交于点
，另一条直角边与直线
、直线分别交于点
、点
．
（1）如图，当点在射线上时，
①求证： 
；
②设
，
，求
与
的函数解析式并写出函数的定义域；
（2）连结
，当△
与△
似时，求
的长．
二次函数
的图像的顶点为
，与
轴交于点
，以
为边在第二象限内作等边三角形
．
（1）求直线的表达式和点
的坐标；
（2）点
在第二象限，且△
的面积等于△的面积，求点
的坐标；
（3）以
轴上的点
为圆心，1为半径的圆，与以点为圆心，
的长为半径的圆相切，直接写出点的坐标．
如图，四边形
中，
∥
，点
在
的延长线上，联结
，交
于点
，联结
，
，且
．
（1） 求证：
；
（2）当
平分
时，求证：四边形是菱形．