二次函数 的图像的顶点为
的图像的顶点为 ,与
,与 轴交于点
轴交于点 ,以
,以 为边在第二象限内作等边三角形
为边在第二象限内作等边三角形 .
.
(1)求直线 的表达式和点
的表达式和点 的坐标;
的坐标;
(2)点 在第二象限,且△
在第二象限,且△ 的面积等于△
的面积等于△ 的面积,求点
的面积,求点 的坐标;
的坐标;
(3)以 轴上的点
轴上的点 为圆心,1为半径的圆,与以点
为圆心,1为半径的圆,与以点 为圆心,
为圆心, 的长为半径的圆相切,直接写出点
的长为半径的圆相切,直接写出点 的坐标.
的坐标.
(本题8分)某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
计 划购进电视机和洗衣机共100台,商店最多可筹集资金160 800元.
划购进电视机和洗衣机共100台,商店最多可筹集资金160 800元.(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其它费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后
 获得利润最多?并求出最多利润.(利润=售价-进价)
获得利润最多?并求出最多利润.(利润=售价-进价)
(本题8分)某校八年级200名女生在体育测试中进行了立定跳远的测试.现从200名女生中随 机抽取10名女生进行测试,下面是她们测试结果的条形统计图.(另附某校八年级女生立定跳远的计分标准)
机抽取10名女生进行测试,下面是她们测试结果的条形统计图.(另附某校八年级女生立定跳远的计分标准)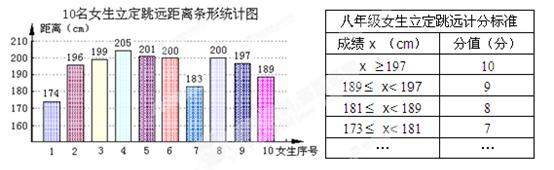
(1)求这10名女生立定跳远距离的中位数,立定跳远得分的众数和平均数.
(2)请你估计该校200名女生在立定跳远测试中得10分的人数.
(本题9分)如图,在平面直角坐标系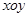 中,
中,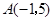 ,
,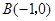 ,
,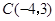 .
.
(1)求出
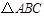 的面积.
的面积.(2)在图中作出
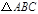 关于
关于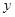 轴的轴对称图形
轴的轴对称图形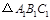 .
.(3)写出点
 的坐标.
的坐标.
(本题9分)已知△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM="CN,直线BN与AM相交于点Q。下面给出了三种情况(如图" ①,②,③),请回答下列问题: 
(1)利用图①证明
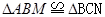 。
。(2)先用量角器分别测量∠BQM的大小,然后猜测∠BQM是否为定值?利用图③证明你的猜想
.(本题8分)学生若干人分住在若干间宿舍,如果每间住4人,那么20人没有宿舍住,如果每间住8人,那么有一间宿舍不空也不满,求学生的人数和宿舍的间数。