如图,已知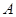 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且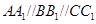 ,
,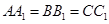 .
.
(1)求证:平面 //平面
//平面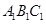 ;
;
(2)若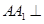 平面
平面 ,且
,且 ,
, ,
,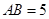 ,求证:
,求证: 平面
平面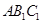 ;
;
(3)在(2)的条件下,求二面角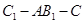 的余弦值.
的余弦值.
已知△ABC的周长为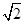 +1,且sin A+sin B=
+1,且sin A+sin B=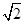 sin C.
sin C.
(1)求边AB的长;
(2)若△ABC的面积为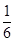 sin C,求角C的度数.
sin C,求角C的度数.
已知函数f(x)=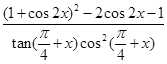
(1)求f(-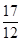 π)的值;
π)的值;
(2)当x∈[0,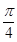 )∪(
)∪(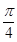 ,
,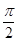 ]时,求g(x)=
]时,求g(x)=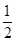 f(x)+sin2x的最大值和最小值.
f(x)+sin2x的最大值和最小值.
已知函数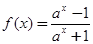 ,其中
,其中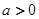 且
且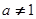 .
.
(1) 判断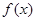 的奇偶性;
的奇偶性;
(2) 判断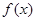 在
在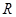 上的单调性,并加以证明.
上的单调性,并加以证明.
已知不等式x2-2x-3<0的解集为A,不等式x2+4x-5<0的解集为B.
(1)求A∪B;
(2)若不等式x2+ax+b<0的解集是A∪B,求ax2+x+b 0的解集.
0的解集.
一个盒子中有2个红球和1个白球,每次取一个.
(1)若每次取出后放回,连续取两次,记A=“取出两球都是红球”,B=“第一次取出红球,第二次取出白球”,求概率P(A),P(B);
(2)若每次取出后不放回,连续取2次,记C=“取出的两球都是红球”,D=“取出的两个球中恰有1个是红球”,求概率P(C),P(D).