如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.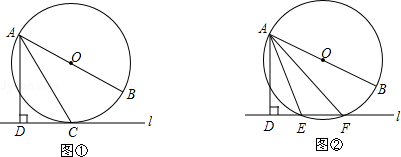
(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.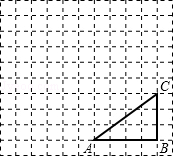
(1)在正方形网格中,作出△AB1C1;(不要求写作法)
(2)设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留π).
在1个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外,其余都相同),其中有白球2个,黄球1个,若从中任意摸出一个球,这个球是白色的概率为0.5.
(1)求口袋中红球的个数;
(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分,甲从口袋中摸出一个球,不放回,再找出一个画树状图的方法求甲摸的两个球且得2分的概率.