某品牌汽车4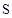
店经销
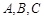三种排量的汽车，其中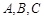三种排量的汽车依次有５，4，3款不同车型．某单位计划购买3辆不同车型的汽车，且购买每款车型等可能．
(1)求该单位购买的3辆汽车均为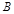
种排量汽车的概率；
(2)记该单位购买的3辆汽车的排量种数为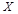
，求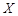
的分布列及数学期望．
设函数
.
（Ⅰ）解不等式
；
（Ⅱ）求函数
的最小值.
在直角坐标系
中，直线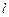
的参数方程为
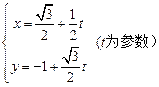，曲线C的参数方程为
.
（Ⅰ）将曲线C的参数方程转化为普通方程；
（Ⅱ）若直线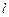与曲线C相交于A、B两点，试求线段AB的长.
如右图所示，AB为⊙O的直径，BC、CD为⊙O的切线，B、D为切点.
（Ⅰ）求证；AD∥OC；
（Ⅱ）若⊙O的半径为1，求AD·OC的值.
已知函数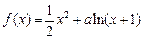
.
（Ⅰ）当
时，求函数
的单调区间和极值；
（Ⅱ）若
在
上是单调递增函数，求实数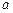
的取值范围.
一盒子中有8个大小完全相同的小球，其中3个红球，2个白球，3个黑球.
（Ⅰ）若不放回地从盒中连续取两次球，每次取一个，求在第一次取到红球的条件下，第二次也取到红球的概率；
（Ⅱ）若从盒中任取3个球，求取出的3个球中红球个数X的分布列和数学期望.