已知a1=1,a2=4,an+2=4an+1+an,bn= ,n∈N+.
,n∈N+.
(1)求b1,b2,b3的值.
(2)设cn=bnbn+1,Sn为数列{cn}的前n项和,求证: Sn≥17n.
(3)求证:|b2n-bn|< ·
· .
.
设函 数
数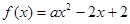 ,对于满足
,对于满足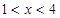 的一切
的一切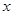 值都有
值都有 ,求实数
,求实数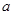 的取值范围。
的取值范围。
已知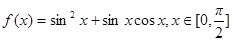
(1)求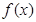 的值域;
的值域;
(2)若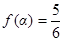 ,求
,求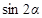 的值。
的值。
(本小题满分14分)已知 的图像在点
的图像在点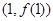 处的切线与直线
处的切线与直线 平行.
平行.
(1)求a,b满足的关系式;
(2)若 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
(3)证明: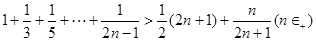
(本小题满分12分)已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为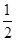 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;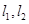 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,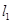 交E于A,B两点,
交E于A,B两点, 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。
(1)求椭圆E的方程;
(2)求 k的取值范围;
k的取值范围;
(3)求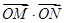 的取值范围。
的取值范围。
(本小题满分12分)
在数列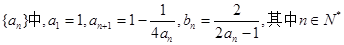 。
。
(1)求证:数列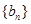 是等差数列,并求数列
是等差数列,并求数列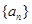 的通项公式
的通项公式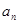 ;
;
(2)设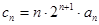 ,求数列
,求数列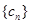 的前
的前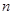 项和。
项和。