如图,已知椭圆 :
: 与双曲线
与双曲线 的离心率互为倒数,且
的离心率互为倒数,且
圆 :
: 的圆心是椭圆
的圆心是椭圆 的左顶点,,设圆
的左顶点,,设圆 与椭圆
与椭圆 交于点
交于点 与点
与点 .
.
(1)求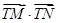 的最小值;
的最小值;
(2)设点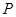 是椭圆
是椭圆 上异于
上异于 ,
, 的任意一点,且直线
的任意一点,且直线 分别与
分别与 轴交于点
轴交于点 ,
, 为坐标原点,求
为坐标原点,求 的最小值.
的最小值.
已知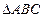 的周长为
的周长为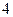 ,且
,且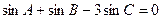 .
.
(I)求边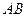 的长.
的长.
(II)若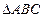 的面积恰为
的面积恰为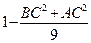 ,①求
,①求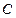 的正弦值. ②求
的正弦值. ②求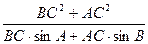 的值.
的值.
正方体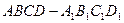 棱长为1,以
棱长为1,以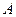 为坐标原点,以直线
为坐标原点,以直线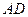 为横轴,直线
为横轴,直线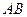 为纵轴,直线
为纵轴,直线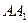 为竖轴建立空间直角坐标系,如图.
为竖轴建立空间直角坐标系,如图. 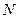 为
为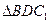 的重心,
的重心,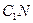
 于
于 .(I)求点
.(I)求点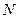 的坐标.(II)求直线
的坐标.(II)求直线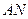 与平面
与平面 所成的角的大小.
所成的角的大小.
已知向量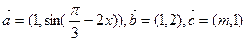
(I)若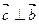 ,求实数
,求实数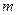 的值.
的值.
(II)若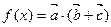 ,①求
,①求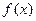 的所有对称轴方程.②求
的所有对称轴方程.②求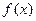 在
在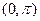 上的单调增区间.
上的单调增区间.
(本小题满分14分)
已知数列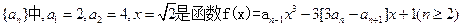 的一个极值点。
的一个极值点。
(1)证明:数列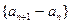 是等比数列;
是等比数列;
(II)求数列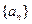 的通项公式;
的通项公式;
(III)设
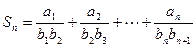 ,求证:
,求证: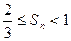
(本小题满分13分)已知点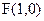 ,直线
,直线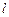 :
: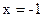 ,
,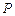 为平面上的动点,过点
为平面上的动点,过点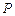 作直线
作直线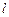 的垂线,垂足为
的垂线,垂足为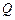 ,且
,且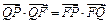 .(1)求动点
.(1)求动点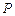 的
的 轨迹
轨迹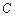 的方程;
的方程;
(2)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD,AE,且AD,AE的斜率k1、k2满足 ,试推断:动直线DE是否过定点?证明你的结论。
,试推断:动直线DE是否过定点?证明你的结论。