7个人排成一排,
(1)甲、乙、丙互不相邻,共有多少咱排法;
(2)甲、乙相邻,丙、丁不相邻,共有多少种排法;
(3)甲不与乙相邻,丙不与乙相邻,有多少种排法.
已知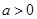 ,求证:
,求证: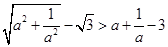
有甲,乙两班进行数学考试,按照大于等于80分为优秀,80分以下为非优秀统计成绩后,得列联表,已知全部100人中随机抽取1人为优秀的概率为 ,
,
| 优秀 |
非优秀 |
合计 |
|
| 甲班 |
15 |
||
| 乙班 |
25 |
||
| 合计 |
100 |
本题可以参考独立性检验临界值表
(1)请完成上面的列联表;
(2)根据列联表中数据,若按95%的可靠性要求,能否认为“成绩优秀与班级有关系”?
已知函数 的极小值为-8,其导函数的图象过点
的极小值为-8,其导函数的图象过点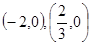 ,如图所示
,如图所示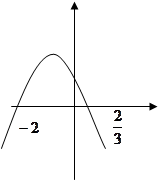
(1)求 的解析式
的解析式
(2)若对 都有
都有 恒成立,求实数的m取值范围。
恒成立,求实数的m取值范围。
设f(x)= ,其中a为正实数.
,其中a为正实数.
(1)当a= 时,求f(x)的极值点;
时,求f(x)的极值点;
(2)若f(x)为R上的单调函数,求a的取值范围.
已知函数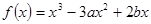 在
在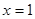 处有极小值-1,求
处有极小值-1,求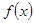 的单调区间.
的单调区间.