已知椭圆
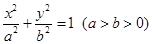的离心率为
，定点
，椭圆短轴的端点是
、
，且
．
（1）求椭圆两焦点与点构成三角形的面积；
（2）设过点
且斜率不为
的直线交椭圆
于
，
两点．试问
轴上是否存在定点
，使
平分
？若存在，求出点的坐标；若不存在，说明理由．
直平行六面体的底面为菱形，过不相邻两条侧棱的截面面积分别为Q1、Q2，求它的侧面积. 
一个正三棱台的上、下底面边长分别是3 cm和6 cm，高是
cm.(1)求三棱台的斜高；(2)求三棱台的侧面积与表面积.
正三棱柱ABC—A1B1C1的底面正△ABC的外接圆半径为
,它的侧棱长为8,求正三棱柱的侧面积.
如图所示棱锥P—ABCD中，底面ABCD是正方形，边长为a，PD=a，PA=PC=
，且PD是四棱锥的高． 
(1)在这个四棱锥中放入一个球，求球的最大半径；
(2)求四棱锥外接球的半径．
在球内有相距1 cm的两个平行截面，截面面积分别是5π cm2和8π cm2，球心不在截面之间，求球面的面积．