已知函数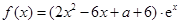 (
(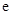 为自然对数的底数).
为自然对数的底数).
(1)求函数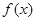 在
在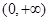 上的单调区间;
上的单调区间;
(2)设函数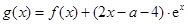 ,是否存在区间
,是否存在区间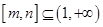 ,使得当
,使得当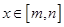 时函数
时函数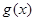 的值域为
的值域为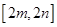 ,若存在求出
,若存在求出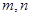 ,若不存在说明理由.
,若不存在说明理由.
已知函数 .
.
(1)求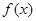 的单调区间和极值点;
的单调区间和极值点;
(2)求使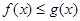 恒成立的实数
恒成立的实数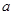 的取值范围;
的取值范围;
(3)当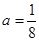 时,是否存在实数
时,是否存在实数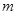 ,使得方程
,使得方程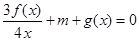 有三个不等实根?若存在,求出
有三个不等实根?若存在,求出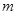 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)已知集合A为 函数 的定义域,
的定义域,
集合 .
.
(I)若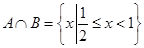 ,求a的值;
,求a的值;
(II)求证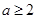 是
是 的充分不必要条件.
的充分不必要条件.
(本小题满分12分) 已知函数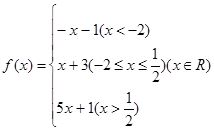 .
.
(1)求函数 的最小值;
的最小值;
(2)已知 ,命题
,命题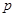 :关于
:关于 的不等式
的不等式
 对任意
对任意 恒成立;
恒成立;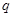 :函数
:函数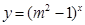 是增函数,若“
是增函数,若“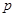 或
或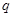 ”为真,“
”为真,“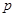 且
且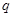 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知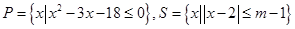
(1)若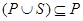 ,求实数m的取值范围;
,求实数m的取值范围;
(2)是否存在实数m,使得“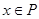 ”是“
”是“ ”的充要条件,若存在,求出m的取值范围;若不存在,请说明理由.
”的充要条件,若存在,求出m的取值范围;若不存在,请说明理由.
(本小题满分12分)(原创)已知点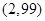 在函数
在函数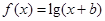 的反函数的图象上.
的反函数的图象上.
(1)求实数 的值;
的值;
(2)若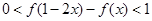 ,求
,求 的取值范围.
的取值范围.