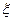在平面直角坐标系 中,已知过点
中,已知过点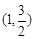 的椭圆
的椭圆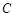 :
: 的右焦点为
的右焦点为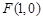 ,过焦点
,过焦点 且与
且与 轴不重合的直线与椭圆
轴不重合的直线与椭圆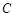 交于
交于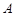 ,
,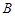 两点,点
两点,点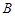 关于坐标原点的对称点为
关于坐标原点的对称点为 ,直线
,直线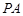 ,
, 分别交椭圆
分别交椭圆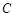 的右准线
的右准线 于
于 ,
, 两点.
两点.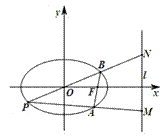
(1)求椭圆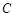 的标准方程;
的标准方程;
(2)若点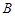 的坐标为
的坐标为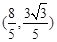 ,试求直线
,试求直线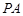 的方程;
的方程;
(3)记 ,
, 两点的纵坐标分别为
两点的纵坐标分别为 ,
,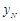 ,试问
,试问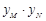 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
(本小题满分12分)如图,多面体ABCDS中,面ABCD为矩形,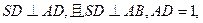
 ,
,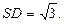

(1)求证:CD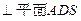 ;
;
(2)求AD与SB所成角的余弦值;
(3)求二面角A—SB—D的余弦值.
已知数列 的前n项和
的前n项和 满足:
满足: (
( 为常数,
为常数,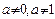 )(Ⅰ)求
)(Ⅰ)求 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设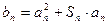 ,若数列
,若数列 为等比数列,求
为等比数列,求 的值;(Ⅲ)在满足条件(Ⅱ)的情形下,
的值;(Ⅲ)在满足条件(Ⅱ)的情形下, ,数列
,数列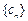 的前n项和为
的前n项和为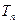 .求证:
.求证: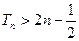 .
.
设 是椭圆
是椭圆 上的两点,已知向量
上的两点,已知向量 ,若
,若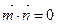 且椭圆的离心率e=,短轴长为
且椭圆的离心率e=,短轴长为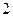 ,
,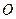 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由
已知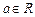 ,函数
,函数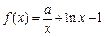 ,
,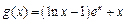 (其中
(其中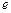 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数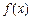 在区间
在区间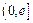 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数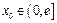 ,使曲线
,使曲线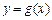 在点
在点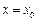 处的切线与
处的切线与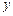 轴垂直? 若存在,求出
轴垂直? 若存在,求出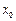 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为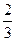 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为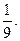 (I)求徒弟加工2个零件都是精品的概率;
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为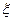 ,求
,求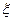 的分布列与均值E
的分布列与均值E