已知函数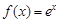 ,
,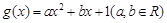 .
.
(1)若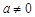 ,则
,则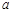 ,
,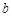 满足什么条件时,曲线
满足什么条件时,曲线 与
与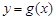 在
在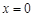 处总有相同的切线?
处总有相同的切线?
(2)当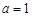 时,求函数
时,求函数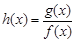 的单调减区间;
的单调减区间;
(3)当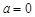 时,若
时,若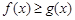 对任意的
对任意的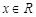 恒成立,求
恒成立,求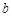 的取值的集合.
的取值的集合.
设两向量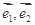 满足
满足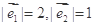 ,
,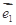 、
、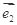 的夹角为
的夹角为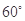 ,
,
(1)试求
(2)若向量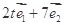 与向量
与向量 的夹角余弦值为非负值,求实数
的夹角余弦值为非负值,求实数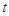 的取值范围.
的取值范围.
已知函数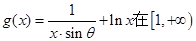 上为增函数,且
上为增函数,且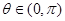 ,
, ,
, .
.
(1)求 的值;
的值;
(2)当 时,求函数
时,求函数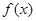 的单调区间和极值;
的单调区间和极值;
(3)若在 上至少存在一个
上至少存在一个 ,使得
,使得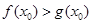 成立,求
成立,求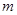 的取值范围.
的取值范围.
已知数列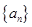 满足
满足
(1)求证:数列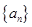 的奇数项,偶数项均构成等差数列;
的奇数项,偶数项均构成等差数列;
(2)求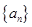 的通项公式;
的通项公式;
(3)设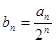 ,求数列
,求数列 的前
的前 项和
项和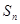 .
.
如图,四棱锥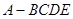 中,
中, 是正三角形,四边形
是正三角形,四边形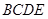 是矩形,且平面
是矩形,且平面 平面
平面 ,
, ,
, .
.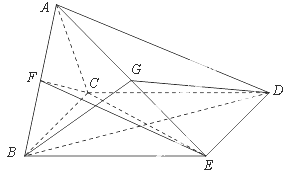
(Ⅰ)若点 是
是 的中点,求证:
的中点,求证: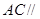 平面
平面 ;
;
(II)试问点 在线段
在线段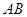 上什么位置时,二面角
上什么位置时,二面角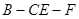 的余弦值为
的余弦值为 .
.
已知定点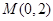 ,
,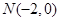 ,直线
,直线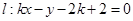 (
( 为常数).
为常数).
(1)若点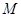 、
、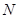 到直线
到直线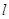 的距离相等,求实数
的距离相等,求实数 的值;
的值;
(2)对于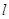 上任意一点
上任意一点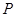 ,
,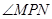 恒为锐角,求实数
恒为锐角,求实数 的取值范围.
的取值范围.