某班高一某班的一次数学测试成绩的茎叶图和频率分布图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
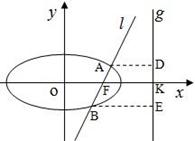
如图,已知直线l:x=my+1过椭圆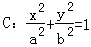 的右焦点F,抛物线:
的右焦点F,抛物线: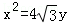 的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且
的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且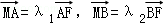 ,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点
,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点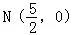 .
.
函数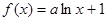
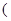
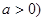 .
.
(1)当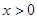 时,求证:
时,求证: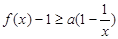 ;
;
(2)在区间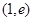 上
上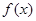
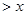 恒成立,求实数
恒成立,求实数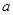 的范围。
的范围。
(3)当 时,求证:
时,求证: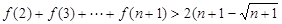 )
)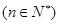 .
.
已知函数f(x)的图象经过点(1,λ),且对任意x∈R,
都有f(x+1)=f(x)+2.数列{an}满足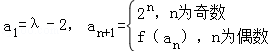 .
.
(1)当x为正整数时,求f(n)的表达式;(2)设λ=3,求a1+a2+a3+…+a2n;
(3)若对任意n∈N*,总有anan+1<an+1an+2,求实数λ的取值范围.
如图,三棱锥P﹣ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分线段PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB.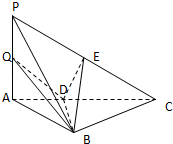
(1)求证:PC⊥平面BDE;
(2)若点Q是线段PA上任一点,判断BD、DQ的位置关系,并证明结论;
(3)若AB=2,求三棱锥B﹣CED的体积.
如图,正方形 的边长为2.
的边长为2.
(1)在其四边或内部取点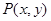 ,且
,且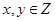 ,求事件:“
,求事件:“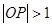 ”的概率;
”的概率;
(2)在其内部取点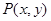 ,且
,且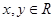 ,求事件“
,求事件“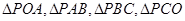 的面积均大于
的面积均大于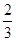 ”的概率.
”的概率.