老王是新农村建设中涌现出的“养殖专业户”.他准备购置80只相同规格的网箱,养殖A、B两种淡水鱼(两种鱼不能混养).计划用于养鱼的总投资不少于7万元,但不超过7.2万元,其中购置网箱等基础建设需要1.2万元.设他用x只网箱养殖A种淡水鱼,目前平均每只网箱养殖A、B两种淡水鱼所需投入及产出情况如下表:
| |
鱼苗投资 (百元) |
饲料支出 (百元) |
收获成品鱼 (千克) |
成品鱼价格 (百元/千克) |
| A种鱼 |
2 |
3 |
100 |
0.1 |
| B种鱼 |
4 |
5 |
55 |
0.4 |
(利润=收入-支出.收入指成品鱼收益,支出包括基础建设投入、鱼苗投资及饲料支出)
(1)按目前市场行情,老王养殖A、B两种淡水鱼获得利润最多是多少万元?
(2)基础建设投入、鱼苗投资、饲料支出及产量不变,但当老王的鱼上市时,A种鱼价格上涨a%,B种鱼价格下降20%,使老王养鱼实际获得利润5.68万元.求a的值.
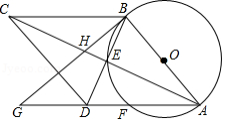
如图, 的对角线 , 交于点 ,以 为直径的 经过点 ,与 交于点 , 是 延长线上一点,连接 ,交 于点 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的直径.
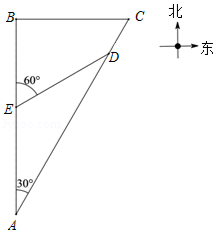
如图,某海岸边有 , 两码头, 码头位于 码头的正东方向,距 码头40海里.甲、乙两船同时从 岛出发,甲船向位于 岛正北方向的 码头航行,乙船向位于 岛北偏东 方向的 码头航行,当甲船到达距 码头30海里的 处时,乙船位于甲船北偏东 方向的 处,求此时乙船与 码头之间的距离.(结果保留根号)
某帐篷厂计划生产10000顶帐篷,由于接到新的生产订单,需提前10天完成这批任务,结果实际每天生产帐篷的数量比计划每天生产帐篷的数量增加了 ,那么计划每天生产多少顶帐篷?
, 两个不透明的盒子里分别装有三张卡片,其中 盒里三张卡片上分别标有数字1,2,3, 盒里三张卡片上分别标有数字4,5,6,这些卡片除数字外其余都相同,将卡片充分摇匀.
(1)从 盒里抽取一张卡、抽到的卡片上标有数字为奇数的概率是 ;
(2)从 盒, 盒里各随机抽取一张卡片,请用列表或画树状图的方法,求抽到的两张卡片上标有的数字之和大于7的概率.
某中学八年级在新学学期开设了四门校本选修课程: .轮滑; .书法; .舞蹈; .围棋,要求每名学生必须选择且只能选择其中一门课程,学校随机抽查了部分八年级学生,对他们的课程选择情况进行了统计,并绘制了如图两幅不完整的统计图.
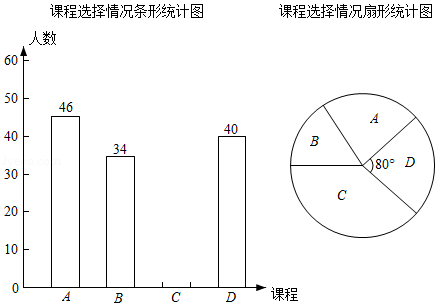
请根据统计图提供的信息,解答下列问题:
(1)此次共抽查了 名学生;
(2)请通过计算补全条形统计图;
(3)若该校八年级共有900名学生,请估计选择 课程的有多少名学生.