已知圆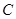 的圆心在直线
的圆心在直线 上,且与直线
上,且与直线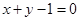 相切于点
相切于点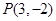 .
.
(Ⅰ)求圆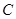 方程;
方程;
(Ⅱ)点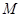
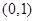 与点
与点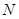 关于直线
关于直线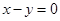 对称.是否存在过点
对称.是否存在过点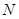 的直线
的直线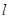 ,
,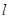 与圆
与圆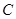 相交于
相交于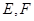 两点,且使三角形
两点,且使三角形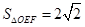 (
(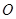 为坐标原点),若存在求出直线
为坐标原点),若存在求出直线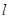 的方程,若不存在用计算过程说明理由.
的方程,若不存在用计算过程说明理由.
(本小题满分12分)有一种新型的洗衣液,去污速度特别快.已知每投放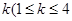 且
且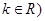 个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度 (克/升)随着时间
(克/升)随着时间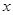 (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为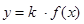 ,其中
,其中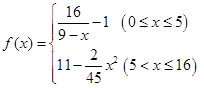 .根据经验,当水中洗衣液的浓度不低于
.根据经验,当水中洗衣液的浓度不低于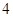 (克/升)时,它才能起到有效去污的作用.
(克/升)时,它才能起到有效去污的作用.
(Ⅰ)若投放 个单位的洗衣液,
个单位的洗衣液,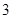 分钟时水中洗衣液的浓度为
分钟时水中洗衣液的浓度为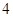 (克/升),求
(克/升),求 的值 ;
的值 ;
(Ⅱ)若投放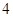 个单位的洗衣液,则有效去污时间可达几分钟?
个单位的洗衣液,则有效去污时间可达几分钟?
(本小题满分12分)在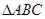 中,内角
中,内角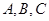 所对的边分别为
所对的边分别为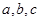 ,已知
,已知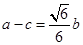 ,
,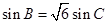 .
.
(Ⅰ)求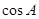 的值;
的值;
(Ⅱ)求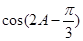 的值.
的值.
(本小题满分14分)已知 ,函数
,函数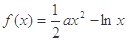 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点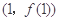 处的切线的斜率;
处的切线的斜率;
(Ⅱ)讨论 的单调性;
的单调性;
(Ⅲ)是否存在实数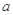 ,使得方程
,使得方程 有两个不等的实数根?若存在,求出
有两个不等的实数根?若存在,求出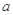 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本小题满分13分)已知数列 ,
,  满足条件:
满足条件:
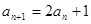 ,
,  .
.
(Ⅰ)求证数列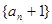 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和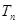 ,并求使得
,并求使得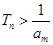 对任意
对任意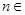
 都成立的正整数
都成立的正整数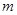 的最小值.
的最小值.
(本小题满分12分)如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间均设有1米宽的走道,已知三块绿化区的总面积为200平方米,求该矩形区域ABCD占地面积的最小值.