在平面直角坐标系中，O为坐标原点，点A坐标为（1，0），以OA为边在第一象限内作等边△OAB，C为x轴正半轴上的一个动点（OC＞1），连接BC，以BC为边在第一象限内作等边△BCD，直线DA交y轴于E点．
（1）如图，当C点在x轴上运动时，设AC＝x，请用x表示线段AD的长；
（2）随着C点的变化，直线AE的位置变化吗？若变化，请说明理由；若不变，请求出直线AE的解析式．
（3）以线段BC为直径作圆，圆心为点F，
①当C点运动到何处时直线EF∥直线BO？此时⊙F和直线BO的位置关系如何？请说明理由．
②G为CD与⊙F的交点，H为直线DF上的一个动点，连结HG、HC，求HG＋HC的最小值，并将此最小值用x表示．
计算：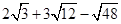
如图1，正方形ABCD中，点H在BC上，连接DH交正方形对角线AC于点E，过点E作DH的垂线交线段AB、CD于点F、G。
（1）求证：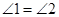
（2）判断DH、FG的数量关系，并说明理由；
（3）在图1中，延长FG与BC交于点P，连接DF、DP（如图2），试探究DF与DP的关系，并说明理由。
如图，已知一个边长分别为6、8、10的直角三角形，请设计出一个有一条边长为8的直角三角形，使这两个直角三角形能够拼成一个等腰三角形。
（1）画出4种不同拼法（周长不等）的等腰三角形；
（2）求出4种不同拼法的图形的等腰三角形的周长。
如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于点F。
（1）找出图中与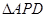
全等的三角形，并说明理由；
（2）猜想三条线段PC、PE、PF之间的比例关系，并说明理由。
课堂上对关于x的方程：
的解进行合作探究时，甲同学发现，当m=0时，方程的两根都为1，当m>0时，方程有两个不相等的实数根；乙同学发现，无论m取什么正实数时方程的两根都不可能相等；丙同学发现无论m取什么正实数时方程的两根这和均为定值。
（1）请找一个m的值代入方程使方程的两个根为互不相等的整数，并求这两个根；
（2）请选择乙或丙同学的发现加以判断，并说明理由。