在平面直角坐标系 中,已知
中,已知 分别是椭圆
分别是椭圆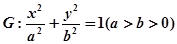 的左、右焦点,椭圆
的左、右焦点,椭圆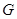 与抛物线
与抛物线 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
.
(Ⅰ)求椭圆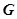 的方程;
的方程;
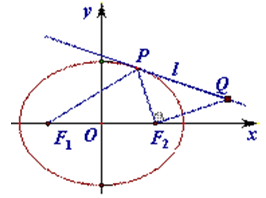
(Ⅱ)设点 是椭圆
是椭圆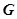 在第一象限上的任一点,连接
在第一象限上的任一点,连接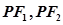 ,过
,过 点作斜率为
点作斜率为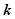 的直线
的直线 ,使得
,使得 与椭圆
与椭圆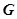 有且只有一个公共点,设直线
有且只有一个公共点,设直线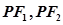 的斜率分别为
的斜率分别为 ,
, ,试证明
,试证明 为定值,并求出这个定值;
为定值,并求出这个定值;
(III)在第(Ⅱ)问的条件下,作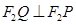 ,设
,设 交
交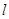 于点
于点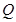 ,
,
证明:当点 在椭圆上移动时,点
在椭圆上移动时,点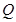 在某定直线上.
在某定直线上.
在直角坐标系xOy中,圆C的参数方程 为参数).以O为极点,
为参数).以O为极点,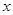 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆C的交点为O,P,与直线
与圆C的交点为O,P,与直线 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
如图,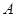 、
、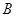 、
、 是圆
是圆 上三点,
上三点,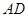 是
是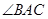 的角平分线,交圆
的角平分线,交圆 于
于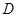 ,过
,过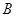 作圆
作圆 的切线交
的切线交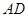 的 延长线于
的 延长线于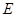 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求证: .
.
已知函数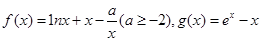 ,其中e为自然对数的底数,且当x>0时
,其中e为自然对数的底数,且当x>0时 恒成立.
恒成立.
(Ⅰ)求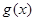 的单调区间;
的单调区间;
(Ⅱ)求实数a的所有可能取值的集合;
(Ⅲ)求证: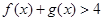 .
.
已知椭圆C长轴的两个顶点为A(-2,0),B(2,0),且其离心率为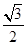 .
.
(Ⅰ)求椭圆C的标准方程;
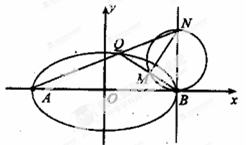
(Ⅱ)若N是直线x=2上不同于点B的任意一点,直线AN与椭圆C交于点Q,设直线QB与以NB为直径的圆的一个交点为M(异于点B),求证:直线NM经过定点.
某市为准备参加省中学生运动会,对本市甲、乙两个田径队的所有跳高运动员进行了测试,用茎叶图表示出甲、乙两队运动员本次测试的跳高成绩(单位:cm,且均为整数),同时对全体运动员的成绩绘制了频率分布直方图.跳高成绩在185cm以上(包括185cm)定义为“优秀”,由于某些原因,茎叶图中乙队的部分数据丢失,但已知所有运动员中成绩在190cm以上(包括190cm)的只有两个人,且均在甲队. 
(Ⅰ)求甲、乙两队运动员的总人数a及乙队中成绩在[160,170)(单位:cm)内的运动员人数b;
(Ⅱ)在甲、乙两队全体成绩为“优秀”的运动员的跳高成绩的平均数和方差;
(Ⅲ)在甲、乙两队中所有的成绩为“优秀”的运动员中随机选取2人参加省中学生运动会正式比赛,
求所选取两名运动员均来自甲队的概率.