经调查统计,某种型号的汽车在匀速行驶中,每小时的耗油量 (升)关于行驶速度
(升)关于行驶速度 (千米/时)的函数可表示为
(千米/时)的函数可表示为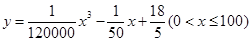 .已知甲、乙两地相距
.已知甲、乙两地相距 千米,在匀速行驶速度不超过
千米,在匀速行驶速度不超过 千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为
千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为 (升).
(升).
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)讨论函数 的单调性,当
的单调性,当 为多少时,耗油量
为多少时,耗油量 为最少?最少为多少升?
为最少?最少为多少升?
设数列{ }的前
}的前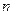 项和为
项和为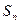 ,且方程
,且方程 有一根为
有一根为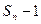 ,
,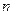 =1,2,3,….
=1,2,3,….
(1)求 ;
;
(2)猜想数列{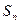 }的通项公式,并给出严格的证明.
}的通项公式,并给出严格的证明.
某种产品的广告费支出 与销售额(单位:百万元)之间有如下对应数据:
与销售额(单位:百万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
50 |
60 |
70 |
如果 与
与 之间具有线性相关关系.
之间具有线性相关关系.
(1)作出这些数据的散点图;(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额.
设函数 ,曲线
,曲线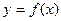 在点(
在点( ,
,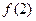 )处的切线方程为
)处的切线方程为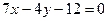 .
.
(1)求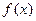 的解析式;
的解析式;
(2)证明:曲线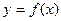 任一点处的切线与直线
任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
、从某高校新生中随机抽取100名学生,测得身高情况(单位: )并根据身高评定
)并根据身高评定 其发育标准如右表所示:
其发育标准如右表所示: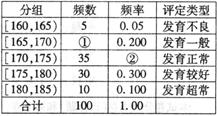
(1)请在频率分布表中的①、②位置上填上相应的数据,估计该批新生中发育正常或较好的概率;
(2)按身高分层抽样,现已抽取20人准备参加世博会志愿者活动,其中有3名学生担任迎宾工作,记“这3名学生中身高低于170 的人数
的人数 ”为
”为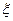 ,求
,求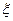 的分布列及期望.
的分布列及期望.
、已知关于x的一元二次函数 ,设集合
,设集合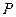 ={1,2,3},
={1,2,3},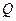 ={-1,1,2,3,4,},分别从集合
={-1,1,2,3,4,},分别从集合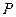 和
和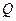 中随机取一个数作为
中随机取一个数作为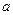 和
和 .
.
(1)求函数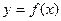 有零点的概率;
有零点的概率;
(2)求函数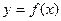 在区间[1,+∞)上是增函数的概率.
在区间[1,+∞)上是增函数的概率.