某跨国饮料公司对全世界所有人均GDP(即人均纯收入)在0.5—8千美元的地区销售,该公司M饮料的销售情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数中(x表示人均GDP,单位:千美元;y表示年人均M饮料的销量,单位:升),用哪个来描述人均,饮料销量与地区的人均GDP的关系更合适?说明理由.
A.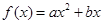 |
B.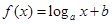 |
C.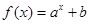 |
D.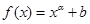 |
(2)若人均GDP为1千美元时,年人均M饮料的销量为2升;人均GDP为4千美元时,年人均M饮料的销量为5升;把你所选的模拟函数求出来.;
(3)因为M饮料在N国被检测出杀虫剂的含量超标,受此事件影响,M饮料在人均GDP不高于3千美元的地区销量下降5%,不低于6千美元的地区销量下降5%,其他地区的销量下降10%,根据(2)所求出的模拟函数,求在各个地区中,年人均M饮料的销量最多为多少?
函数f(x)= (a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立?为什么?
(3)在直角坐标系中,求定点A(–3,1)到此函数图象上任意一点P的距离|AP|的最小值。
已知不等式x2–3x+t<0的解集为{x|1<x<m, mÎR}
(1)求t, m的值;
(2)若f(x)= –x2+ax+4在(–∞,1)上递增,求不等式log a (–mx2+3x+2–t)<0的解集。
设函数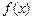 在
在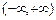 上满足
上满足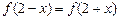 ,
, 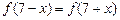 且在闭区间[0, 7]上只有
且在闭区间[0, 7]上只有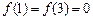 .
.
⑴试判断函数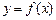 的奇偶性;
的奇偶性;
⑵试求方程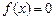 在闭区间
在闭区间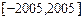 上的根的个数, 并证明你的结论.
上的根的个数, 并证明你的结论.
命题甲:  R, 关于x的方程
R, 关于x的方程 有两个非零实数解;
有两个非零实数解;
命题乙:  R, 关于x的不等式
R, 关于x的不等式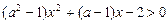 的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
集合A是由具备下列性质的函数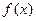 组成的:
组成的:
(1) 函数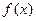 的定义域是
的定义域是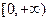 ;
;
(2) 函数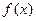 的值域是
的值域是 ;
;
(3) 函数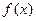 在
在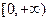 上是增函数.试分别探究下列两小题:
上是增函数.试分别探究下列两小题:
(Ⅰ)判断函数 ,及
,及 是否属于集合A?并简要说明理由.
是否属于集合A?并简要说明理由.
(Ⅱ)对于(I)中你认为属于集合A的函数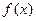 ,不等式
,不等式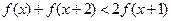 ,是否对于任意的
,是否对于任意的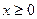 总成立?若不成立,为什么?若成立,请证明你的结论.
总成立?若不成立,为什么?若成立,请证明你的结论.