已知数列 的前
的前 项和为
项和为 满足
满足 .
.
(Ⅰ)函数 与函数
与函数 互为反函数,令
互为反函数,令 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(Ⅱ)已知数列 满足
满足 ,证明:对任意的整数
,证明:对任意的整数 ,有
,有 .
.
(本小题满分10分)选修4—5:不等式选讲
已知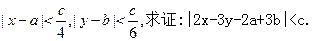
(本小题满分10分)选修4—4:坐标与参数方程
已知直线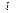 经过点P(1,1),且
经过点P(1,1),且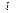 的一个方向向量
的一个方向向量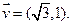
(I)写出直线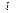 的参数方程;
的参数方程;
(II)设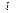 与圆
与圆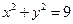 相交于两点A、B,求点P到A、B两点间的距离之积。
相交于两点A、B,求点P到A、B两点间的距离之积。
(本小题满分10分)选修4—1:几何证明选讲
如图,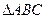 内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D。
内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D。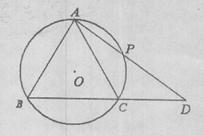 (I)求证:
(I)求证: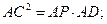
(II)若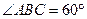 ,⊙O的半径为1,
,⊙O的半径为1,
且P为弧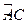 的中点,求AD的长。
的中点,求AD的长。
(本小题满分12分)函数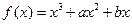 的图象C与x轴相切于不同于原点的一点,且
的图象C与x轴相切于不同于原点的一点,且 的极小值为-4。
的极小值为-4。
(I)求函数 的解析式及单调区间;
的解析式及单调区间;
(II)过曲线C上一点 (P1不是C的对称中心)作曲线C的切线,切C于不同于
(P1不是C的对称中心)作曲线C的切线,切C于不同于 的另一点
的另一点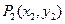 ,再过
,再过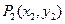 作曲线C的切线,切C于不同于
作曲线C的切线,切C于不同于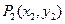 的另一点
的另一点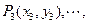 过
过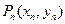 作曲线C的切线,切C于不同于
作曲线C的切线,切C于不同于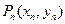 的另一点
的另一点 令
令 的通项公式。
的通项公式。
(本小题满分12分)某市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩; (III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为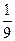 ,求甲在初赛中答题个数的分布列及数学期望。
,求甲在初赛中答题个数的分布列及数学期望。