已知二次函数f(x)满足:①在x=1时有极值;②图象过点(0,-3),且在该点处的切线与直线2x+y=0平行.
⑴求f(x)的解析式;
⑵求函数g(x)=f(x2)的单调递增区间.
(本小题满分12分)
已知数列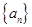 是公差大于零的等差数列,数列
是公差大于零的等差数列,数列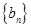 为等比数列,且
为等比数列,且
(1)求数列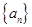 和
和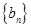 的通项公式
的通项公式
(2)设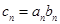 ,求数列
,求数列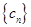 前n项和
前n项和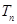 .
.
已知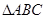 中,a,b, c 为角A,B,C 所对的边,
中,a,b, c 为角A,B,C 所对的边, .
.
(1)求cos A的值;
(2)若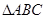 的面积为
的面积为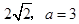 ,求b ,c 的长.
,求b ,c 的长.
设函数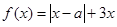 ,其中
,其中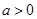 .
.
(1)当 时,求不等式
时,求不等式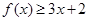 的解集;
的解集;
(2)若不等式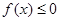 的解集为
的解集为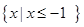 ,求
,求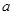 的值.
的值.
已知曲线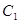 的参数方程为
的参数方程为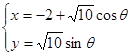 (
(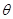 为参数),曲线
为参数),曲线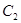 的极坐标方程为
的极坐标方程为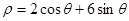 .
.
(1)将曲线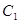 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线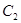 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)曲线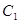 ,
,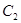 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
如图,A,B,C,D四点在同一圆上,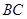 与
与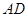 的延长线交于点
的延长线交于点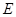 ,点
,点 在
在 的延长线上.
的延长线上.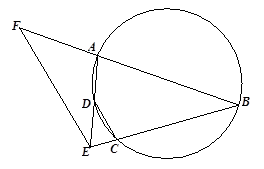
(1)若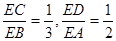 ,求
,求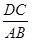 的值;
的值;
(2)若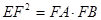 ,证明:
,证明: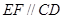 .
.