已知曲线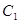 的参数方程为
的参数方程为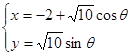 (
(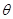 为参数),曲线
为参数),曲线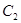 的极坐标方程为
的极坐标方程为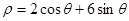 .
.
(1)将曲线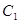 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线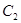 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)曲线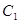 ,
,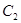 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
已知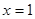 是函数
是函数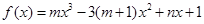 的一个极值点,其中
的一个极值点,其中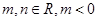 .
.
(1)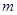 与
与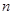 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)当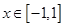 时,函数
时,函数 的图象上任意一点处的切线的斜率恒大于
的图象上任意一点处的切线的斜率恒大于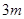 ,求
,求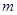 的取值范围.
的取值范围.
在平面直角坐标系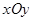 中,动点
中,动点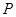 到两点
到两点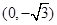 、
、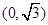 的距离之和等于4.设点
的距离之和等于4.设点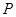 的轨迹为
的轨迹为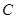 .
.
(1)求曲线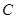 的方程;
的方程;
(2)设直线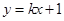 与
与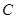 交于
交于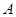 、
、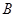 两点,若
两点,若 ,求
,求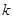 的值.
的值.
如图,在直三棱柱中 -A BC中,AB
-A BC中,AB  AC,AB=AC=2,
AC,AB=AC=2,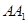 =4,点D是BC的中点.
=4,点D是BC的中点.
(1)求异面直线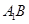 与
与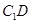 所成角的余弦值;
所成角的余弦值;
(2)求平面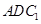 与
与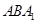 所成二面角的正弦值.
所成二面角的正弦值.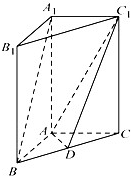
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(1)求张同学至少取到1道乙类题的概率;
(2)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对每道甲类题的概率都是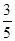 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是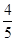 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用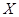 表示张同学答对题的个数,求
表示张同学答对题的个数,求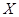 的分布列和数学期望.
的分布列和数学期望.
已知等差数列 的前
的前 项和为
项和为 ,
, ,
,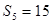 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)若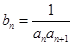 ,求数列
,求数列 的前100项和.
的前100项和.