已知点(1,2)是函数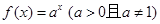 的图象上一点,数列
的图象上一点,数列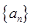 的前
的前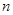 项和
项和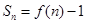 .
.
(Ⅰ)求数列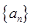 的通项公式;
的通项公式;
(Ⅱ)若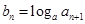 ,求数列
,求数列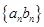 的前
的前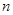 项和
项和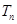 .
.
已知函数 .
.
(1)求函数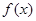 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)求函数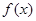 在
在 上的最小值.
上的最小值.
设已知函数 ,
,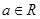 .
.
(1)当 时,求函数
时,求函数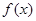 的最大值的表达式
的最大值的表达式 .
.
(2)是否存在实数 ,使得
,使得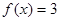 有且仅有3个不等实根,且它们成等差数列,若存在,求出所有
有且仅有3个不等实根,且它们成等差数列,若存在,求出所有 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知抛物线 的方程为
的方程为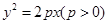 ,点
,点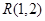 在抛物线
在抛物线 上.
上.
(1)求抛物线 的方程;
的方程;
(2)过点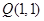 作直线交抛物线
作直线交抛物线 于不同于
于不同于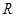 的两点
的两点 ,
,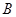 ,若直线
,若直线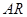 ,
,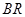 分别交直线
分别交直线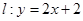 于
于 ,
, 两点,求
两点,求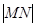 最小时直线
最小时直线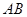 的方程.
的方程.
如图,三棱锥 中,
中, 平面
平面 ,
, ,点
,点 ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2) 在线段
在线段 上的点,且
上的点,且 平面
平面 .
.
①确定点 的位置;
的位置;
②求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
已知正项数列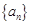 的前
的前 项和为
项和为 ,且
,且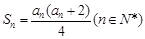 .
.
(1)求数列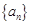 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列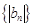 的前
的前 项和.
项和.