设函数 的定义域是
的定义域是 ,对于任意的
,对于任意的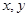 ,有
,有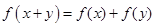 ,且当
,且当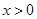 时,
时,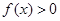 .
.
(1)求 的值;
的值;
(2)判断函数的奇偶性;
(3)用函数单调性的定义证明函数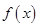 为增函数;
为增函数;
(4)若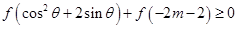 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知集合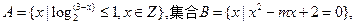 若
若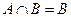 ,求实数m的取值范围。
,求实数m的取值范围。
(本小题满分14分)
已知二次函数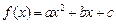 , 满足
, 满足 且
且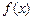 的最小值是
的最小值是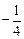 .
.
(Ⅰ)求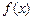 的解析式;
的解析式;
(Ⅱ)设直线 ,若直线
,若直线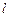 与
与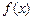 的图象以及
的图象以及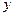 轴这二条直线和一条曲线所围成封闭图形的面积是
轴这二条直线和一条曲线所围成封闭图形的面积是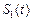 , 直线
, 直线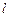 与
与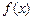 的图象以及直线
的图象以及直线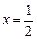 这二条直线和一条曲线所围成封闭图形的面积是
这二条直线和一条曲线所围成封闭图形的面积是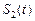 ,已知
,已知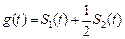 ,当
,当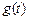 取最小值时,求
取最小值时,求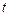 的值.
的值.
(本小题满分14分第一.第二小问满分各7分)
已知向量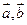 满足
满足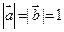 ,且
,且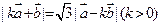 ,令
,令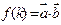 ,
,
(Ⅰ)求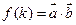 (用
(用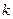 表示);
表示);
(Ⅱ)当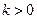 时,
时,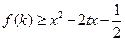 对任意的
对任意的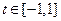 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分14分)
如图,四棱锥P-ABCD是底面边长为1的正方形,PD⊥BC,PD=1,PC=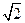 .
.
(Ⅰ)求证:PD⊥面ABCD;
(Ⅱ)求二面角A-PB-D的大小.
(本小题满分12分)
在△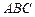 中,
中,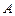 ,
,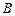 ,
,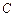 是三角形的三内角,a,b,
是三角形的三内角,a,b,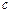 是三内角对应的三边长,已知
是三内角对应的三边长,已知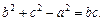
(Ⅰ)求角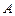 的大小;
的大小;
(Ⅱ)若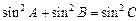 ,求角
,求角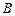 的大小.
的大小.