注:此题选A题考生做①②小题,选B题考生做①③小题.
已知函数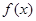 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当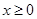 时有
时有 .
.
①求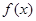 的解析式;②(选A题考生做)求
的解析式;②(选A题考生做)求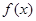 的值域;
的值域;
③(选B题考生做)若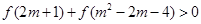 ,求
,求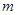 的取值范围.
的取值范围.
在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格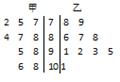
(1)用样本估计总体,请根据茎叶图对甲乙两个班级的成绩进行比较。
(2)求从甲班10名学生和乙班10名学生中各抽取一人,已知有人及格的条件下乙班同学不及格的概率;
(3)从甲班10人中抽取一人,乙班10人中抽取二人,三人中及格人数记为X,求X的分布列和期望。
如图所示,在四棱锥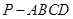 中,底面ABCD为菱形,
中,底面ABCD为菱形, , Q为AD的中点.
, Q为AD的中点.
(Ⅰ)若 ,求证:平面
,求证:平面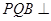 平面
平面 ;
;
(Ⅱ)点M在线段PC上,若平面
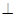 平面ABCD,且
平面ABCD,且 ,三棱锥的体积
,三棱锥的体积 ,
,
求二面角 的大小.
的大小.
已知等差数列 的前
的前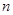 项和为
项和为 ,
, 为等比数列,且
为等比数列,且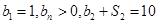 ,
,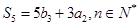 。
。
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)求数列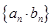 的前n项和
的前n项和 。
。
在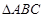 中,角
中,角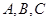 的对边分别为
的对边分别为 且
且
(1)求 的值;
的值;
(2)若 ,且
,且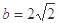 ,求
,求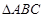 的面积.
的面积.
已知函数 .
.
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若关于 的不等式
的不等式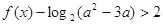 恒成立,求实数
恒成立,求实数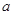 的取值范围.
的取值范围.