如图所示,在四棱锥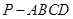 中,底面ABCD为菱形,
中,底面ABCD为菱形, , Q为AD的中点.
, Q为AD的中点.
(Ⅰ)若 ,求证:平面
,求证:平面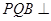 平面
平面 ;
;
(Ⅱ)点M在线段PC上,若平面
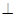 平面ABCD,且
平面ABCD,且 ,三棱锥的体积
,三棱锥的体积 ,
,
求二面角 的大小.
的大小.
为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,
将他们的候车时间(单位:分钟)作为样本分成5组,如表所示:
| 组别 |
候车时间 |
人数 |
| 一 |
[0,5) |
2 |
| 二 |
[5,10) |
6 |
| 三 |
[10,15) |
4 |
| 四 |
[15,20) |
2 |
| 五 |
[20,25) |
1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
已知函数 ,
,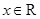 .
.
(1)求 的值;
的值;
(2)若 ,
,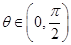 ,求
,求
椭圆的两个焦点分别为 ,离心率
,离心率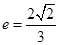 。
。
(1)求椭圆方程;
(2)一条不与坐标轴平行的直线 与椭圆交于不同的两点
与椭圆交于不同的两点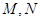 ,且线段
,且线段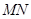 中点的横坐标为
中点的横坐标为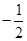 ,求直线
,求直线 倾斜角的取值范围。
倾斜角的取值范围。
设函数 的图象在点
的图象在点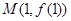 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)求函数 的单调递增区间,并求函数
的单调递增区间,并求函数 在
在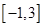 上的最大值和最小值。
上的最大值和最小值。
已知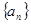 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,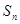 表示
表示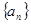 的前
的前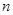 项和。
项和。
(1)求 及
及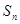 ;
;
(2)设数列 的前
的前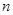 项和为
项和为 ,求证:当
,求证:当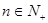 都有
都有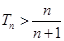 成立。
成立。