已知函数 .
.
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若关于 的不等式
的不等式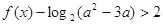 恒成立,求实数
恒成立,求实数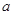 的取值范围.
的取值范围.
(本小题满分12分)已知函数
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2) 时,令
时,令 .求
.求 在
在 上的最大值和最小值;
上的最大值和最小值;
(3)若函数 对
对
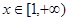 恒成立,求实数
恒成立,求实数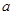 的取值范围.
的取值范围.
(本小题满分12分)已知函数f(x)=2x3+ax2+bx+3在x=-1和x=2处取得极值.
(1)求f(x)的表达式和极值;
(2)若f(x)在区间[m,m+4]上是单调函数,试求m的取值范围.
(本小题满分12分)在△ABC中,a、b、c分别为角A、B、C的对边, .
.
(1)求角C;
(2)若边c=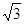 ,a+b=3,求边a和b的值.
,a+b=3,求边a和b的值.
(本小题满分12分)f(x)=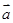 .
. ,其中向量
,其中向量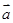 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),
=(1+sin2x,1), ,且函数
,且函数 的图象经过点
的图象经过点 .
.
(Ⅰ)求实数 的值.
的值.
(Ⅱ)求函数 的最小值及此时
的最小值及此时 值的集合.
值的集合.
(本小题满分12分)已知等比数列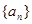 中,
中,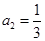 ,公比
,公比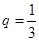 ,
,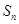 为
为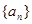 的前
的前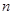 项和.
项和.
(1)求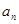 和Sn
和Sn
(2)设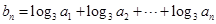 ,求数列
,求数列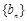 的通项公式.
的通项公式.