设点 、
、 分别是椭圆
分别是椭圆 的左、右焦点,
的左、右焦点, 为椭圆
为椭圆 上任意一点,且
上任意一点,且 的最小值为
的最小值为 .
.
(I)求椭圆 的方程;
的方程;
(II)设直线 (直线
(直线 、
、 不重合),若
不重合),若 、
、 均与椭圆
均与椭圆 相切,试探究在
相切,试探究在 轴上是否存在定点
轴上是否存在定点 ,使点
,使点 到
到 、
、 的距离之积恒为1?若存在,请求出点
的距离之积恒为1?若存在,请求出点 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
已知非零向量 满足
满足 ,且
,且 .
.
(1)求 ; (2)当
; (2)当 时,求向量
时,求向量 与
与 的夹角
的夹角 的值.
的值.
设函数
 ,其中向量
,其中向量 ,
, ,且函数
,且函数 的图象经过点
的图象经过点 .
.
(1)求实数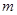 的值;(2)求函数
的值;(2)求函数 的最小值及此时
的最小值及此时 的值的集合.
的值的集合.
设函数 图像的一条对称轴是直线
图像的一条对称轴是直线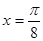 .
.
(1)求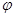 ;(2)画出函数
;(2)画出函数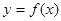 在区间
在区间 上的图像(在答题纸上完成列表并作图).
上的图像(在答题纸上完成列表并作图).
已知二次函数 .
.
(1)若 ,试判断函数
,试判断函数 零点个数;
零点个数;
(2)是否存在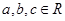 ,使
,使 同时满足以下条件
同时满足以下条件
①对任意 ,且
,且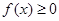 ;
;
②对任意 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(3)若对任意 且
且 ,
, ,试证明存在
,试证明存在 ,
,
使 成立。
成立。
设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业。分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(0<x<100)。而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元。
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?