在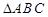 中,角
中,角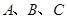 所对的边分别为
所对的边分别为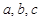 ,且
,且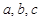 成等比数列.
成等比数列.
(1)若 ,
,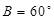 ,求
,求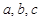 的值;
的值;
(2)求角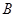 的取值范围.
的取值范围.
(本小题满分12分)在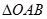 中,已知点
中,已知点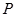 为线段
为线段 上的一点,且
上的一点,且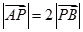 .
.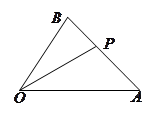
(1)试用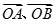 表示
表示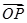 ;
;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(本小题12分)已知sin(2α-β)=  ,sinβ=" -"
,sinβ=" -" 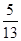 ,且α∈(
,且α∈(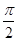 ,π),β∈(-
,π),β∈(-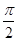 ,0),求sinα的值.
,0),求sinα的值.
已知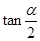 =2,求值:
=2,求值:
(1) ;
;
(2)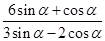 .
.
如图,分别以菱形BCED的对角线BE、CD所在直线为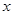 轴、
轴、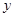 轴建立平面直角坐标系,抛物线
轴建立平面直角坐标系,抛物线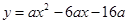 (
(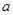 <0)过B、C两点,与
<0)过B、C两点,与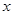 轴的负半轴交于点A,且∠ACB=90°.点P是
轴的负半轴交于点A,且∠ACB=90°.点P是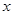 轴上一动点,设点P的坐标为(
轴上一动点,设点P的坐标为(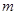 ,0),过点P作直线
,0),过点P作直线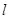 垂直于
垂直于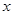 轴,交抛物线于点Q.
轴,交抛物线于点Q.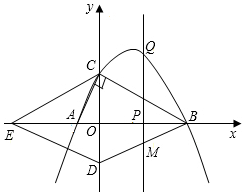
(1)求点A、B、C的坐标及抛物线的解析式;
(2)当点P在线段OB上运动时,直线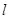 交BD于点M,试探究:
交BD于点M,试探究:
①求MQ的大小;(用含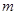 的化简式子表示)
的化简式子表示)
②当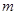 为何值时,四边形CQBM的面积取得最大值,并求出这个最大值.
为何值时,四边形CQBM的面积取得最大值,并求出这个最大值.
(3)当点P在线段EB上运动时,是否存在点 Q,使△BDQ为直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑摩托车从B地到A地,到达A地后立即按原路返回。右图是甲、乙两人离B地的距离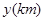 与行驶时间
与行驶时间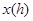 之间的函数图象,根据图象解答以下问题:
之间的函数图象,根据图象解答以下问题:
(1)A、B两地之间的距离为  ;
;
(2)直接写出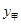 ,
,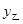 与
与 之间的函数关系式(不必写过程),求出点M的坐标,并解释该点坐标所表示的实际意义;
之间的函数关系式(不必写过程),求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间的距离不超过3 时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲、乙两人能够用无线对讲机保持联系.
时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲、乙两人能够用无线对讲机保持联系.