交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,
8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.
(1)这20个路段轻度拥堵、中度拥堵的路段各有多少个?
(2)从这20个路段中随机抽出的3个路段,用X表示抽取的中度拥堵的路段的个数,求X的分布列及期望.
(本题10分)
已知等差数列 满足
满足 ,
, 为
为 的前
的前 项和.
项和.
(1)求通项 及当
及当 为何值时,
为何值时, 有最大值,并求其最大值。
有最大值,并求其最大值。
(2)设 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前
的通项公式及其前 项和
项和 .
.
(本题10分)
(1) 若集合 ,求
,求 ;
;
(2) 若集合 ,正数
,正数 满足
满足 ,
, 的所有可能取值组成的集合为
的所有可能取值组成的集合为 ,求
,求 。
。
已知函数

(1)判断 的奇偶性并证明;
的奇偶性并证明;
(2)若 的定义域为[
的定义域为[ ](
]( ),判断
),判断 在定义域上的增减性,并加以证明;
在定义域上的增减性,并加以证明;
(3)若 ,使
,使 的值域为[
的值域为[ ]的定义域区间[
]的定义域区间[ ](
]( )是否存在?若存在,求出[
)是否存在?若存在,求出[ ],若不存在,请说明理由.
],若不存在,请说明理由.
(本小题14分)根据市场调查,某商品在最近的20天内的价格 与时间
与时间 满足关系
满足关系 {
{ ,销售量
,销售量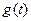 与时间
与时间 满足关系
满足关系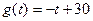 ,
, ,设商品的日销售额为
,设商品的日销售额为 (销售量与价格之积).
(销售量与价格之积).
(1)求商品的日销售额 的解析式;
的解析式;
(2)求商品的日销售额 的最大值.
的最大值.
(本题满分14分,每小题各7分)计算下列各式
(Ⅰ)
(Ⅱ) 