已知椭圆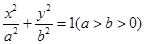 的左、右焦点分别为
的左、右焦点分别为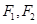 ,离心率为
,离心率为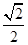 ,P是椭圆上一点,且
,P是椭圆上一点,且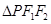 面积的最大值等于2.
面积的最大值等于2.
(1)求椭圆的方程;
(2)过点M(0,2)作直线 与直线
与直线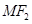 垂直,试判断直线
垂直,试判断直线 与椭圆的位置关系5
与椭圆的位置关系5
(3)直线y=2上是否存在点Q,使得从该点向椭圆所引的两条切线相互垂直?若存在,求点Q的坐标;若不存在,说明理由。
如图,在四棱锥 中,底面
中,底面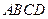 为菱形,
为菱形, ,
,  ,
, 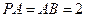 ,
,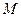 为
为 的中点,
的中点,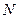 为
为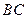 的中点
的中点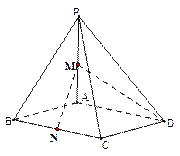
(1)证明:直线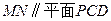
 ;
;
(2)求异面直线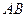 与
与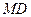 所成角的大小;
所成角的大小;
(3)求点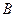 到平面
到平面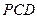 的距离.
的距离.
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为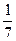 ,现有甲、乙两人从袋中轮流摸取1球.甲先取,乙后取,然后甲再取…取后不放回,每人最多取两次,若两人中有一人首先取到白球时则终止,每个球在每一次被取出的机会是等可能的.
,现有甲、乙两人从袋中轮流摸取1球.甲先取,乙后取,然后甲再取…取后不放回,每人最多取两次,若两人中有一人首先取到白球时则终止,每个球在每一次被取出的机会是等可能的.
(1)求袋中原有白球的个数;
(2)求甲取到白球的概率;
(3)求取球4次终止的概率.
已知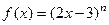 展开式的二项式系数和为512,
展开式的二项式系数和为512,
且
(1)求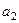 的值;
的值;
(2)求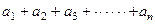 的值;
的值;
(3)求 被6整除的余数.
被6整除的余数.
某同学练习投篮,已知他每次投篮命中率为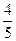 ,
,
(1)求在他第三次投篮后,首次把篮球投入篮框内的概率;
(2)若想使他投入篮球的概率达到0.99,则他至少需投多少次?(lg2=0.3)
在直三棱柱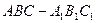 中,
中,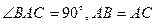 ,直线
,直线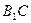 与平面
与平面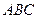 成
成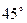 角;
角;
(1)求证:平面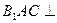 平面
平面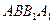 ;
;
(2)求二面角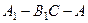 的正弦值.
的正弦值.