如图，已知椭圆C的中心在原点，焦点在x轴上，离心率为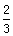
，且过点
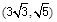，点A、B分别是椭圆C长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于
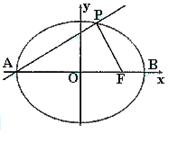
轴上方，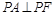
.
（1）求椭圆C的方程；
（2）求点P的坐标；
（3）设M是直角三角PAF的外接圆圆心，求椭圆C上的点到点M的距离
的最小值．
已知f（x）=
.
（1）判断函数的奇偶性；
（2）证明：f（x）是定义域内的增函数；
（3）求f（x）的值域.
已知定义在R上的奇函数f(x)有最小正周期2，且当x∈(0,1)时，f(x)=
.
（1）求f（x)在［-1，1］上的解析式；
（2）证明：f(x)在（0，1）上是减函数.
已知函数f(x)=log2
+log2(x-1)+log2(p-x).
（1）求f(x)的定义域；
（2）求f(x)的值域.
化简求值.
（1）log2
+log212-
log242-1;
(2)(lg2)2+lg2·lg50+lg25;
(3)(log32+log92)·(log43+log83).
已知函数f(x)=logax(a＞0,a≠1)，如果对于任意x∈［3，+∞）都有|f(x)|≥1成立，试求a的取值范围.