已知 通过观察上述不等式的规律,则关于正数
通过观察上述不等式的规律,则关于正数 满足的不等式是
满足的不等式是 .
.
设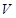 是已知平面
是已知平面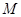 上所有向量的集合,对于映射
上所有向量的集合,对于映射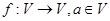 ,记
,记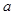 的象为
的象为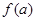 。若映射
。若映射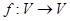 满足:对所有
满足:对所有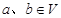 及任意实数
及任意实数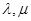 都有
都有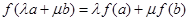 ,则
,则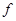 称为平面
称为平面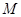 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设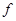 是平面
是平面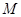 上的线性变换,
上的线性变换,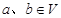 ,则
,则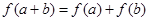 ;
;
②若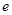 是平面
是平面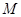 上的单位向量,对
上的单位向量,对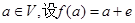 ,则
,则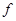 是平面
是平面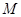 上的线性变换;
上的线性变换;
③对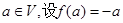 ,则
,则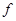 是平面
是平面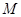 上的线性变换;
上的线性变换;
④设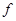 是平面
是平面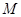 上的线性变换,
上的线性变换, ,则对任意实数
,则对任意实数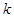 均有
均有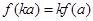 。
。
其中的真命题是.(写出所有真命题的编号)
在△ABC中,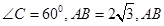 边上的高为
边上的高为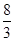 ,则
,则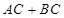 =.
=.
设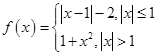 ,则
,则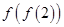 =.
=.
函数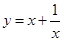 的极大值为 .
的极大值为 .
设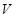 是已知平面
是已知平面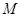 上所有向量的集合,对于映射
上所有向量的集合,对于映射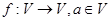 ,记
,记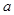 的象为
的象为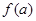 。若映射
。若映射 满足:对所有
满足:对所有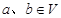 及任意实数
及任意实数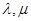 都有
都有 ,则
,则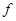 称为平面
称为平面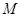 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设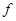 是平面
是平面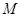 上的线性变换,
上的线性变换,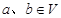 ,则
,则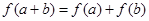 ;
;
②若 是平面
是平面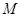 上的单位向量,对
上的单位向量,对 ,则
,则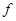 是平面
是平面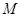 上的线性变换;
上的线性变换;
③对 ,则
,则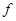 是平面
是平面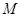 上的线性变换;
上的线性变换;
④设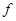 是平面
是平面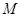 上的线性变换,
上的线性变换, ,则对任意实数
,则对任意实数 均有
均有 。
。
其中的真命题是.(写出所有真命题的编号)