在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为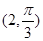 .
.
(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线 的参数方程为
的参数方程为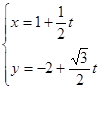 (t为参数),直线
(t为参数),直线 与圆C相交于A,B两点,已知定点
与圆C相交于A,B两点,已知定点 ,求|MA|·|MB|.
,求|MA|·|MB|.
数列{an}的前n项和记为 Sn,a1=2,an+1=Sn+n,等差数列{bn}的各项为正,其前n项和为Tn,且 T3=9,又 a1+b1,a2+b2,a3+b3成等比数列.
(Ⅰ)求{an},{bn}的通项公式;
(Ⅱ)求证:当n≥2时,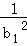 +
+ +…+
+…+ <
< .
.
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(Ⅰ)求取出的3个球编号都不相同的概率;
(Ⅱ)记X为取出的3个球中编号的最小值,求X的分布列与数学期望.
如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(Ⅰ)试证:AB⊥平面BEF;
(Ⅱ)设PA=k•AB,且二面角E﹣BD﹣C的平面角大于45°,求k的取值范围.
(本小题满分13分)
已知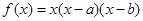 ,点A(s, f(s)), B(t, f(t))
,点A(s, f(s)), B(t, f(t))
(Ⅰ)若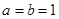 ,求函数
,求函数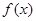 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数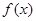 的导函数
的导函数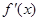 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|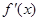 |≤
|≤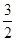 恒成立,求函数
恒成立,求函数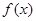 的解析表达式;
的解析表达式;
(Ⅲ)若0<a<b, 函数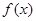 在
在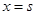 和
和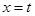 处取得极值,且
处取得极值,且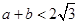 ,证明:
,证明: 与
与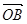 不可能垂直.
不可能垂直.
(本小题满分13分)
设关于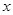 的一元二次方程
的一元二次方程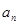
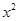
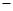
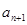
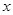
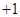
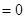 (
(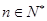 )有两根
)有两根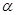 和
和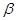 ,且满足
,且满足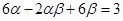 .
.
(Ⅰ)试用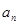 表示
表示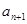 ;
;
(Ⅱ)求证:数列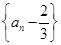 是等比数列;
是等比数列;
(Ⅲ)当 时,求数列
时,求数列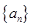 的通项公式,并求数列
的通项公式,并求数列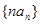 的前
的前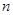 项和
项和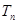 .
.